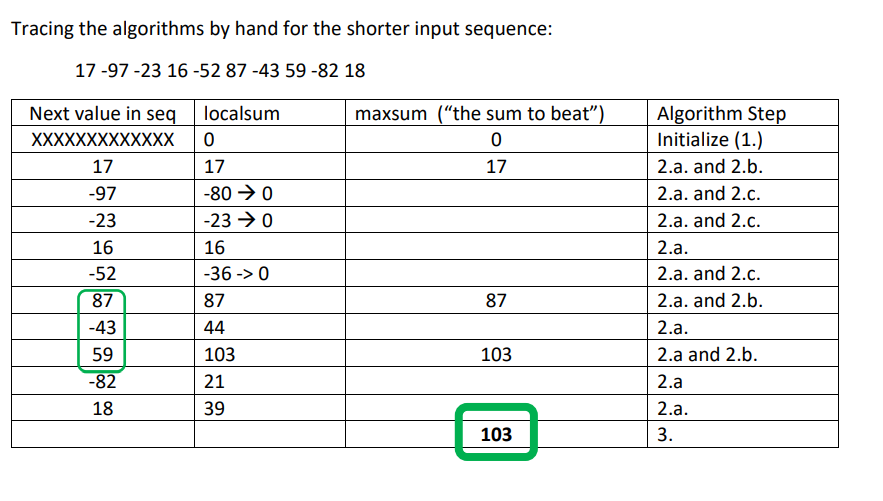
An Efficient Algorithm: Maintain two integer variables, maxsum (to hold the currently maximal sum seen), and localsum (the sum of elements of a currently examined subsequence). 1. Initialize maxsum to 0; initialize localsum to o 2. Traversing an input number sequence Seq from left to right; process each number value V in Seq: a. Add V to localsum b. If localsum is greater than maxsum, update maxsum to the value of local sum ... C. Else: if localsum is negative, reset localsum to 0 3. Report maxsum as the Maximal Subsequence Sum C++ Implementation: (including the subsequences underlying the maximal subsequence sum) Vector max_subseq_sum_collect (const Vector int>& vec, int& max) { int maxsum = 0; int localsum = 0; Vector maxseq; Vector localseq; for (int i = 0; i maxsum) { maxsum = localsum; maxseq = localseq; } else if (localsum 0 87 44 103 21 39 Algorithm Step Initialize (1.) 2.a. and 2.b. 2.a. and 2.c. 2.a. and 2.c. 2.a. 2.a. and 2.c. 2.a. and 2.b. 2.a. 2.a and 2.b. 2.a 2.a. 3. 87 103 103 Question 1: What is the maximal subsequence sum when the input sequence consists of only positive integers? Trace the algorithm (and/or function implementation) for the sequence on only positive values: 17 97 23 16 52 87 43 59 82 18 Next value in seg localsum maxsum ("the sum to beat") Algorithm Step XXXXXXXXXXXXX 0 0 Initialize (1.) Page 3 of 9 Based on your insights gained from the example, answer in general, descriptive terms: (2 pts) Question 2: Using the "Algorithm" or running the C++ implementation, what is the maximal subsequence sum when the input sequence consists of only negative integers? Trace the algorithm (and/or function implementation) for the sequence on only negative values: -17-97-23-16-52-87-43-59-82-18 Next value in seq localsum maxsum ("the sum to beat") Algorithm Step XXXXXXXXXXXXX 0 0 Initialize (1.) The answer you find (specific value): (2 pts) Question 3: Is the answer to Question 2 the correct solution to the problem (where sequence contains only negatives)? ... You should find that not ... i. What is the correct maximal sum result for Question 2: (1 pt) Answer in general, descriptive terms: - (1 pt) Identify the one algorithm step and/or line of code that sets the process up for guaranteed failure for all input sequences of only negative numbers