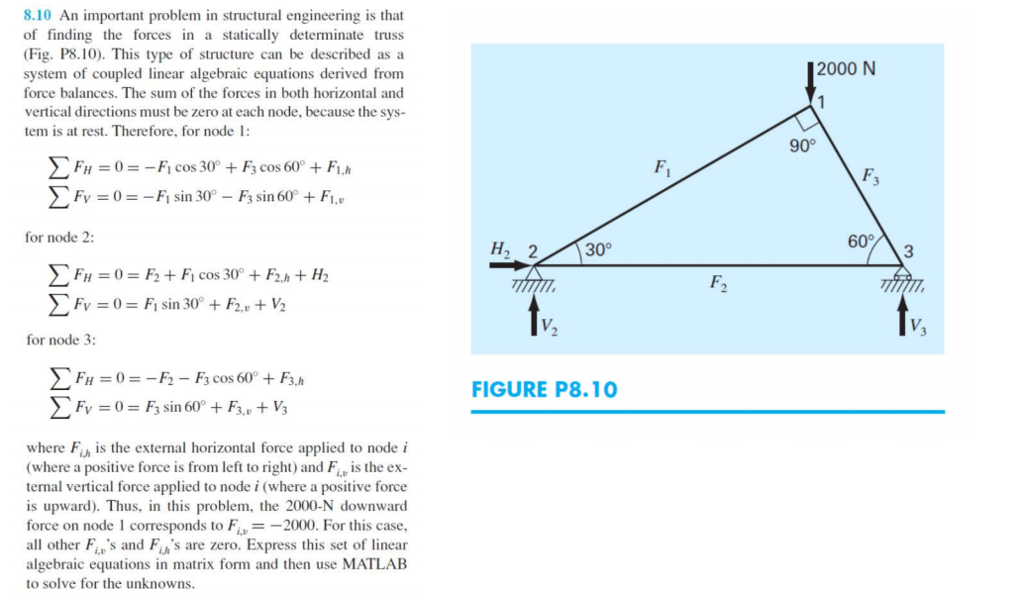
An important problem in structural engineering is that of finding the forces in a statically determinate truss (Fig. P8. 10). This is type of structure can be described as a system of coupled linear algebraic equations derived from force balances. The sum of the forces in both horizontal and vertical directions must be zero at each node, because the system is at rest. Therefore, for node 1: sigma F_h = 0 = - F_1 cos 30degree + F_3 cos 60degree + F_1, h sigma F_v = 0 = - F_1 sin 30degree - F_3 sin60degree + F_1, v for node 2: sigma F_h = 0 = F_2 + F_1 cos 30degree + F_2.h + H_2 sigma F_v = 0 =F_1 sin 30degree + F_+2.v + V_2 for node 3: sigma F_h = 0 = - F_2 - F_3 cos 60degree + F_3, h sigma F_V = 0 = - F_3 sin 60degree + F_3, V_3 where F_i, h is the external horizontal force applied to node i (where a positive force is from left to right) and F_i, v is the external vertical force applied to node i (where a positive force is upward). Thus, in this problem, the 2000-N downward force on node 1 corresponds to F_i v = - 2000. For this case, all other F_I V's and F_i, h' s are zero. Express this set of linear algebraic equations in matrix form and then use MATLAB to solve for the unknowns. An important problem in structural engineering is that of finding the forces in a statically determinate truss (Fig. P8. 10). This is type of structure can be described as a system of coupled linear algebraic equations derived from force balances. The sum of the forces in both horizontal and vertical directions must be zero at each node, because the system is at rest. Therefore, for node 1: sigma F_h = 0 = - F_1 cos 30degree + F_3 cos 60degree + F_1, h sigma F_v = 0 = - F_1 sin 30degree - F_3 sin60degree + F_1, v for node 2: sigma F_h = 0 = F_2 + F_1 cos 30degree + F_2.h + H_2 sigma F_v = 0 =F_1 sin 30degree + F_+2.v + V_2 for node 3: sigma F_h = 0 = - F_2 - F_3 cos 60degree + F_3, h sigma F_V = 0 = - F_3 sin 60degree + F_3, V_3 where F_i, h is the external horizontal force applied to node i (where a positive force is from left to right) and F_i, v is the external vertical force applied to node i (where a positive force is upward). Thus, in this problem, the 2000-N downward force on node 1 corresponds to F_i v = - 2000. For this case, all other F_I V's and F_i, h' s are zero. Express this set of linear algebraic equations in matrix form and then use MATLAB to solve for the unknowns