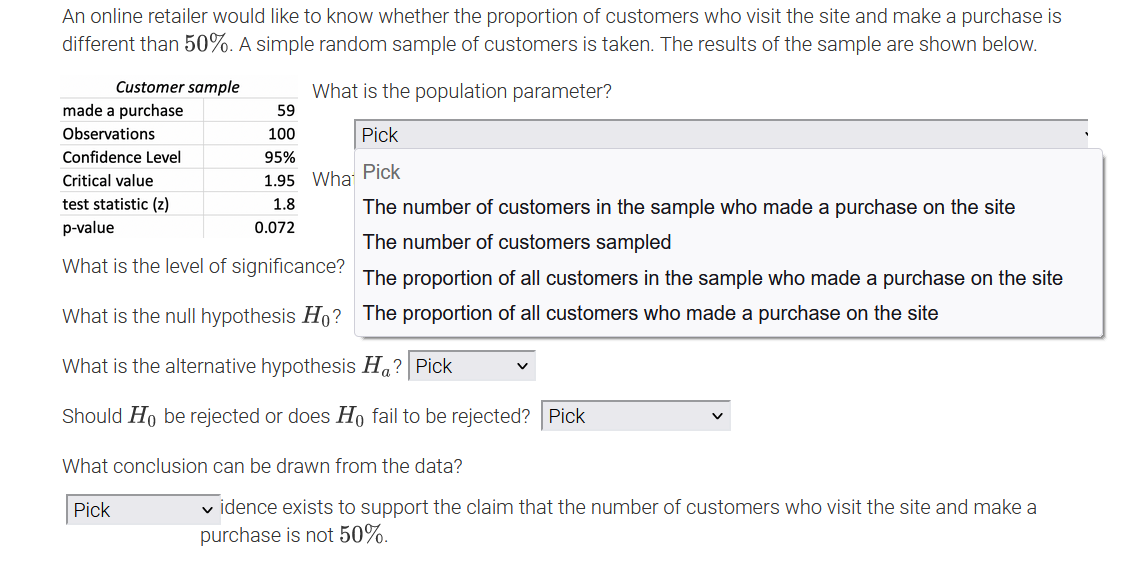
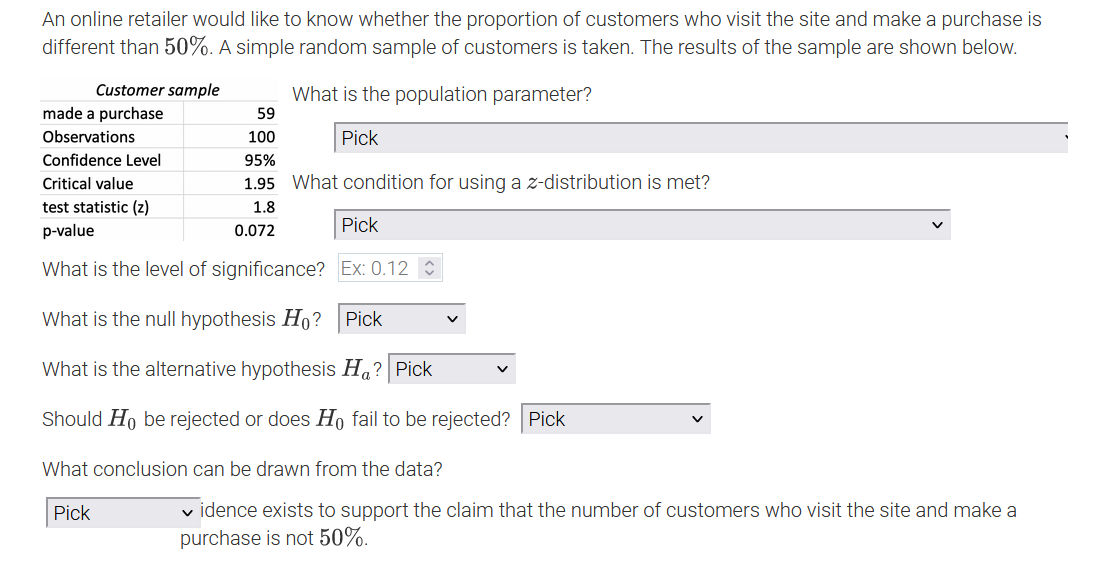
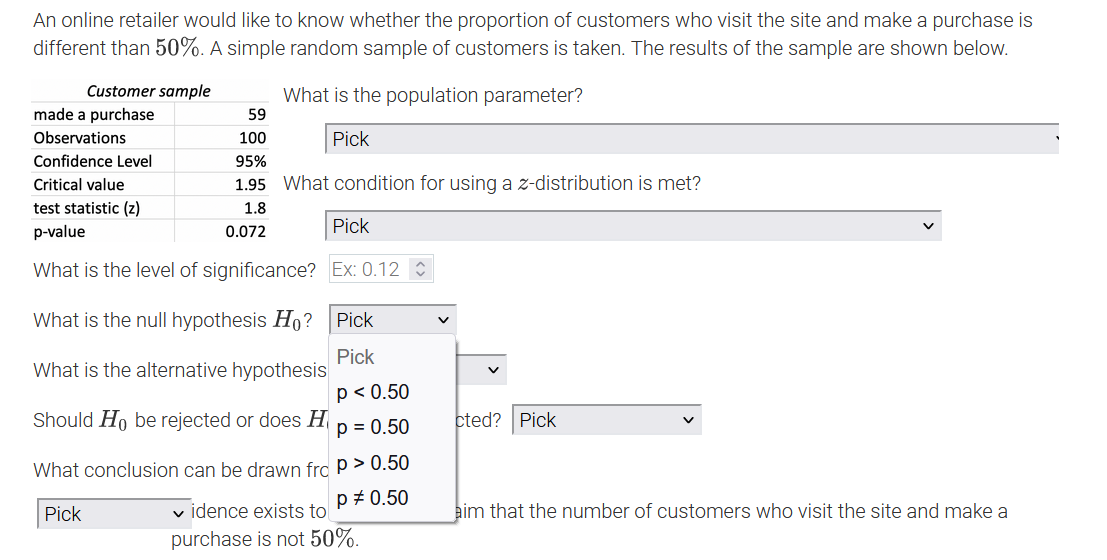
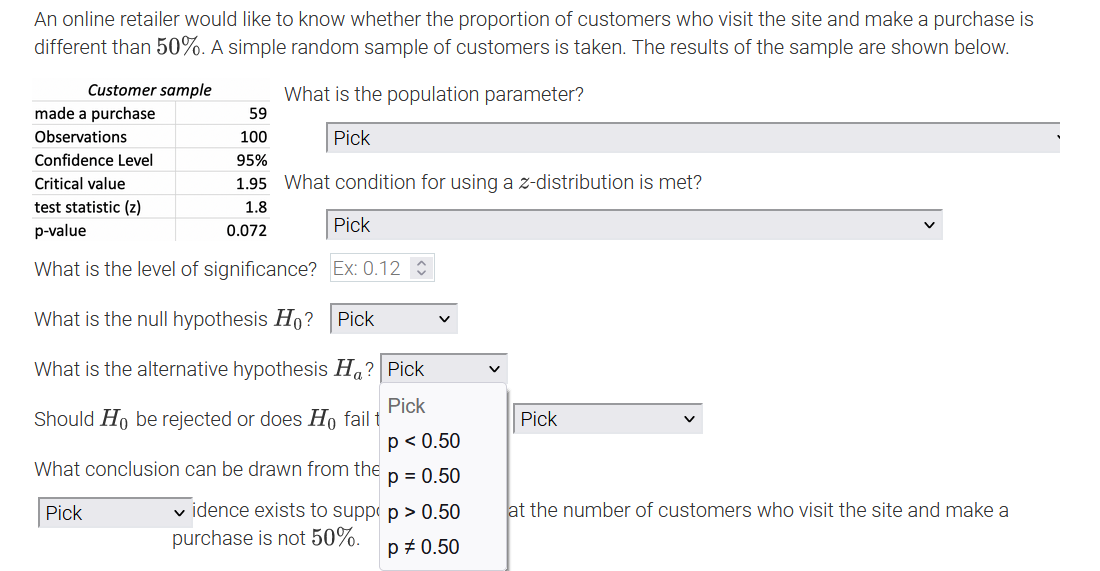
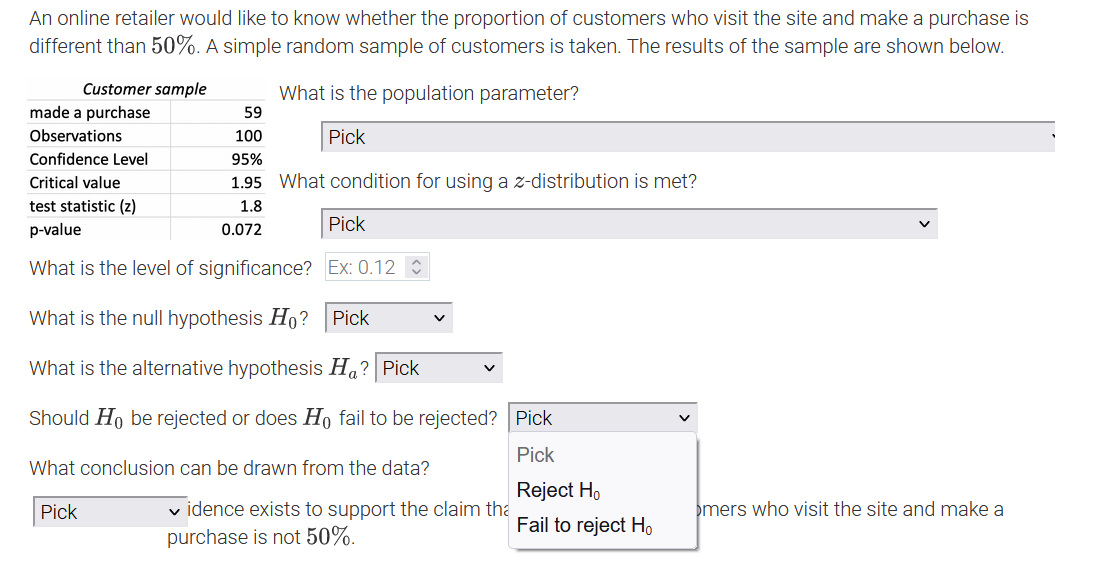
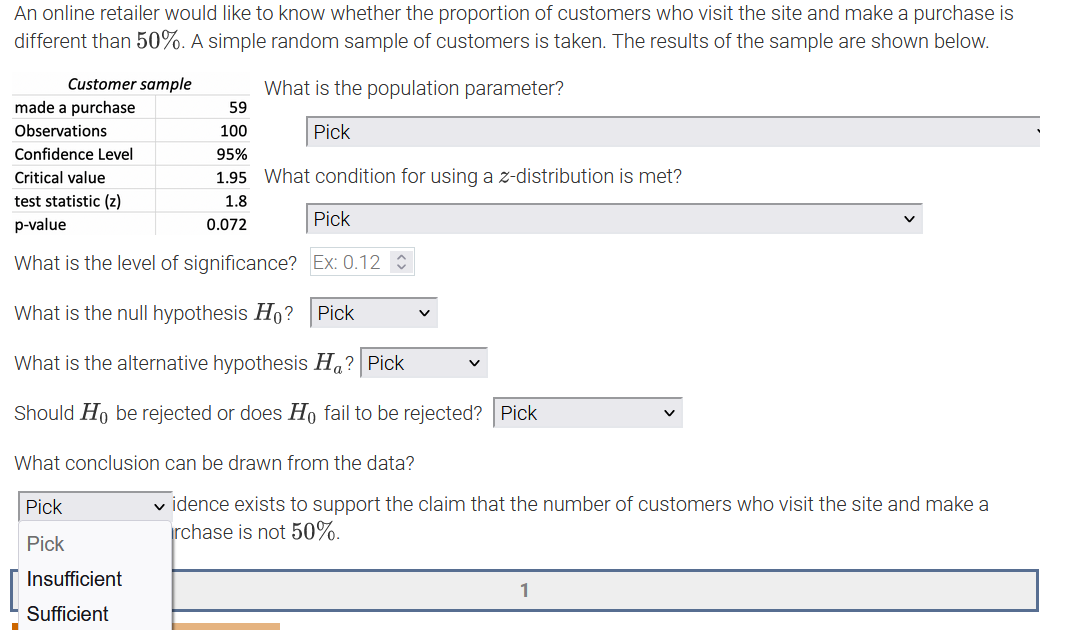
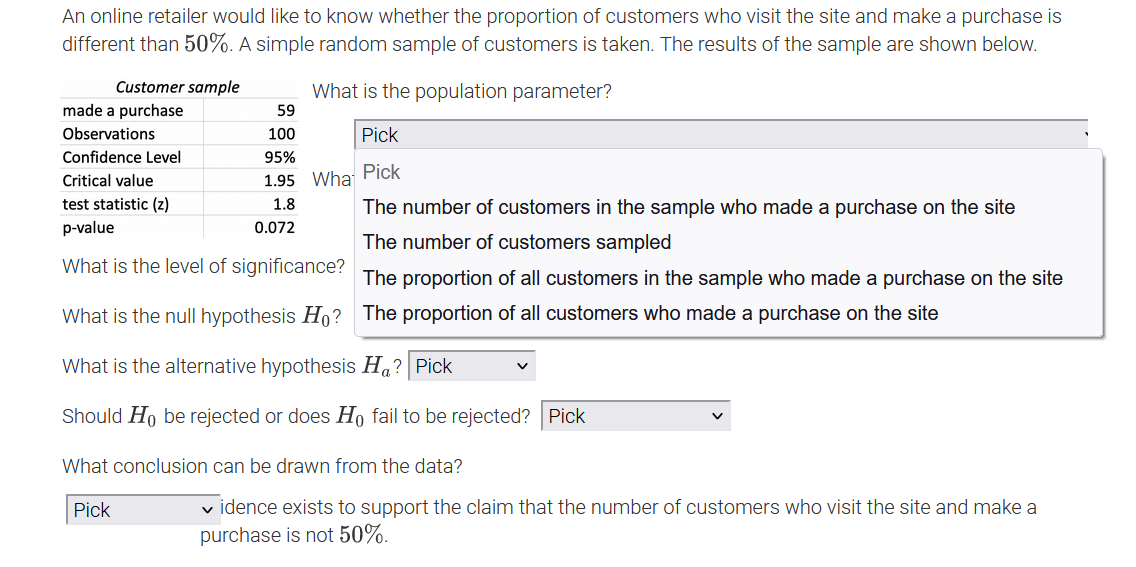
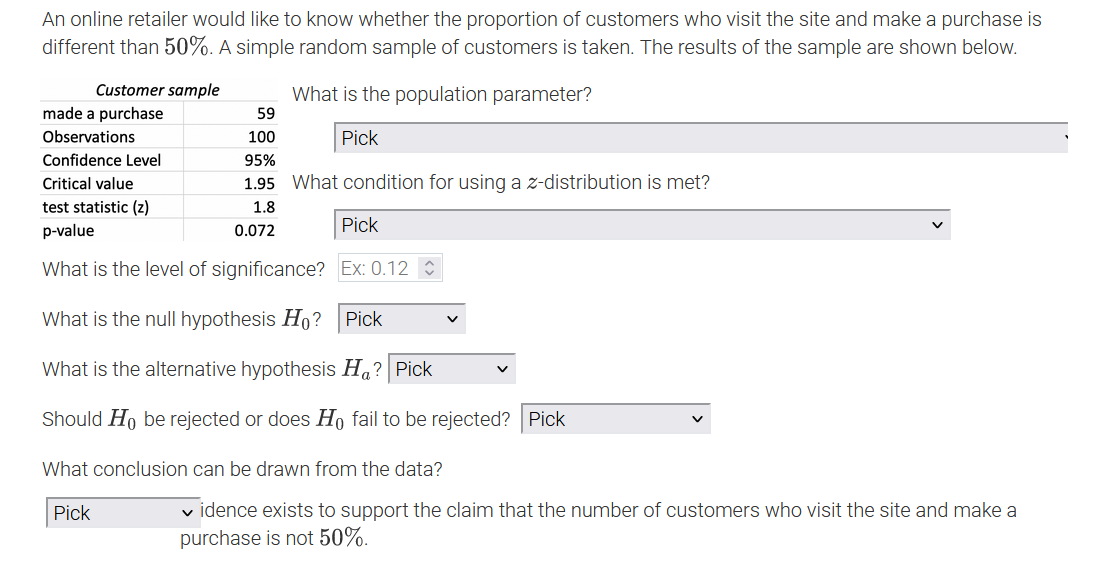
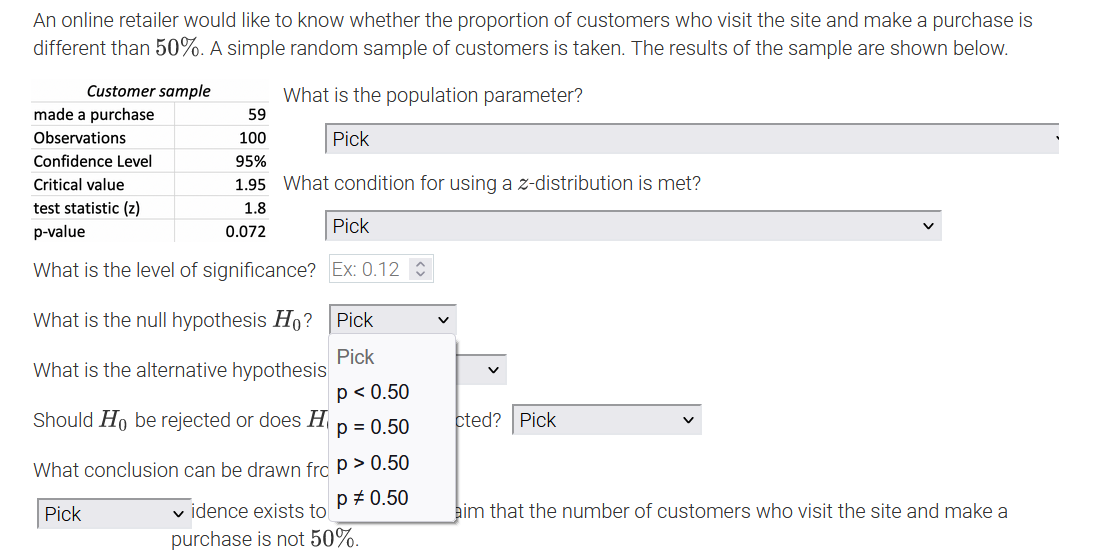
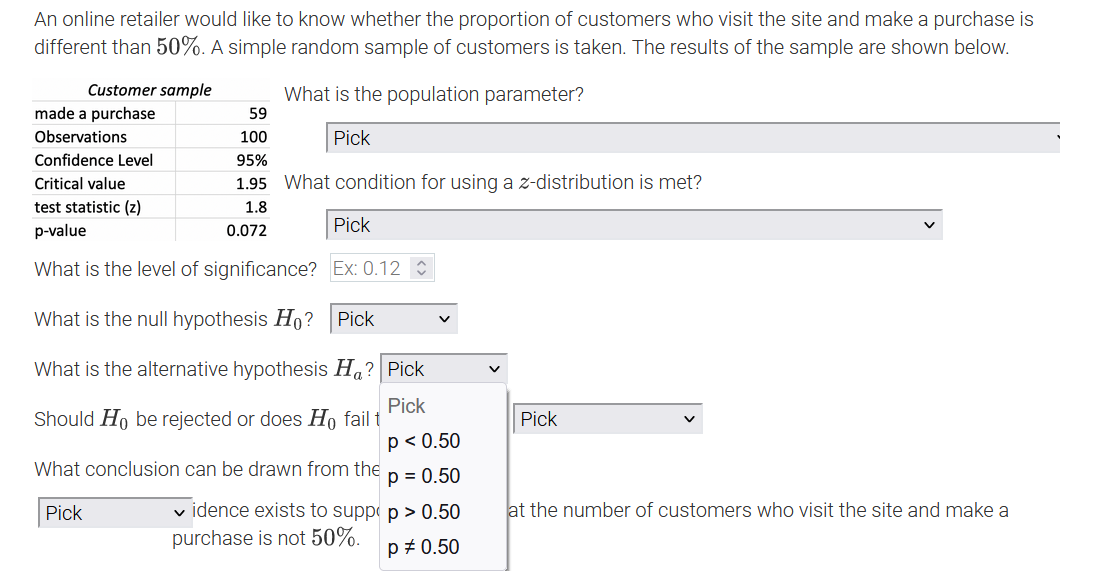
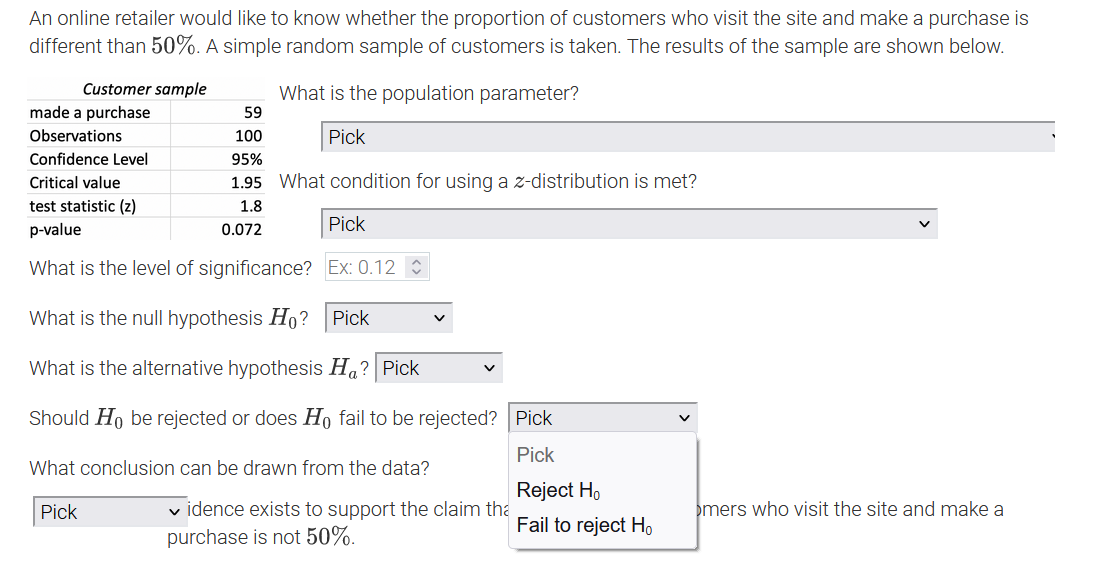
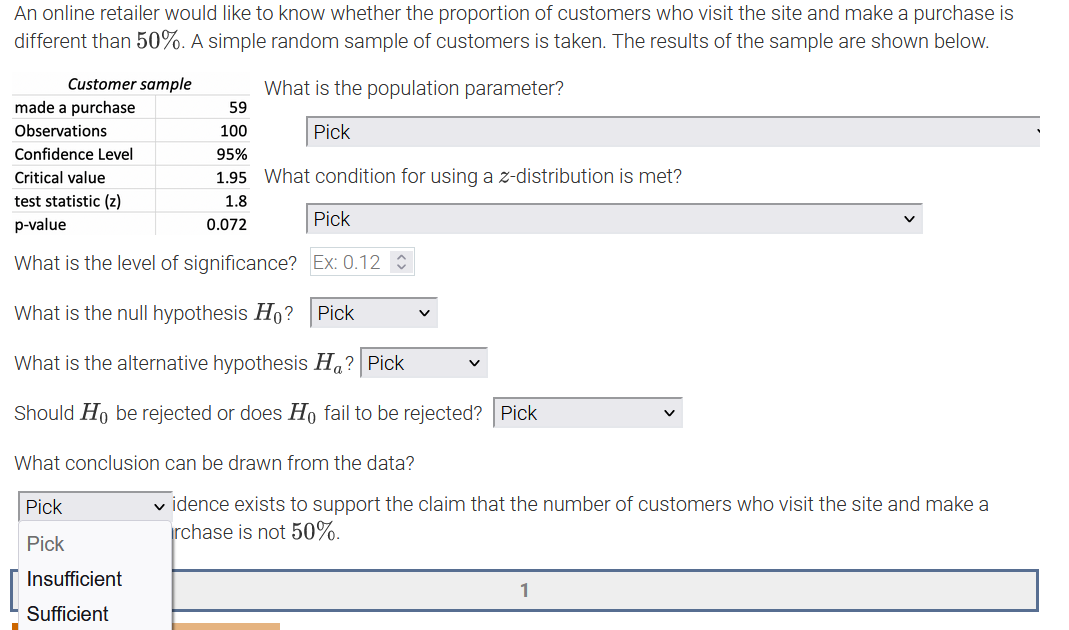
An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What Pick test statistic (z) 1.8 The number of customers in the sample who made a purchase on the site p-value 0.072 The number of customers sampled What is the level of significance? The proportion of all customers in the sample who made a purchase on the site What is the null hypothesis Ho? The proportion of all customers who made a purchase on the site What is the alternative hypothesis Ha? Pick Should Ho be rejected or does Ho fail to be rejected? |Pick What conclusion can be drawn from the data? Pick v idence exists to support the claim that the number of customers who visit the site and make a purchase is not 50%.An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is ta ken? The results of the sample are shown below. Customer sample made a purchase 59 Observations 100 Condence Level 95% Critical value 1.95 test statistic {z} 1.3 p-value 0.072 What is the population parameter? I Pick ' What condition for using a zdistribution is met? I Pick V What is the level of signicance? PiCk What is the null hypothesis H0 ? A simple random sample of more than 30 customers was taken. The sample taken was a simple random sample. What is the alternative hypothesis The true population proportion is known. Should Hg be rejected or does Hg fail to be rejected? I Pick v What conclusion can be drawn from the data? I Pick v idence exists to support the claim that the number of customers who visit the site and make a purchase is not 50%. An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What condition for using a z-distribution is met? test statistic (z) 1.8 p-value 0.072 Pick What is the level of significance? Ex: 0.12 $ What is the null hypothesis Ho? Pick What is the alternative hypothesis Ha? Pick V Should Ho be rejected or does Ho fail to be rejected? Pick What conclusion can be drawn from the data? Pick v idence exists to support the claim that the number of customers who visit the site and make a purchase is not 50%.An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What condition for using a z-distribution is met? test statistic (z) 1.8 p-value 0.072 Pick V What is the level of significance? Ex: 0.12 C What is the null hypothesis Ho? Pick Pick What is the alternative hypothesis V p 0.50 idence exists to p # 0.50 Pick him that the number of customers who visit the site and make a purchase is not 50%.An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What condition for using a z-distribution is met? test statistic (z) 1.8 p-value 0.072 Pick V What is the level of significance? Ex: 0.12 $ What is the null hypothesis Ho? Pick What is the alternative hypothesis H,? Pick Pick Should Ho be rejected or does Ho fail Pick p 0.50 at the number of customers who visit the site and make a purchase is not 50%. p # 0.50An online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What condition for using a z-distribution is met? test statistic (z) 1.8 p-value 0.072 Pick v What is the level of significance? Ex: 0.12 0 What is the null hypothesis Ho? Pick What is the alternative hypothesis Ha? Pick Should Ho be rejected or does Ho fail to be rejected? Pick Pick What conclusion can be drawn from the data? Reject Ho Pick v idence exists to support the claim the mers who visit the site and make a purchase is not 50%. Fail to reject HoAn online retailer would like to know whether the proportion of customers who visit the site and make a purchase is different than 50%. A simple random sample of customers is taken. The results of the sample are shown below. Customer sample What is the population parameter? made a purchase 59 Observations 100 Pick Confidence Level 95% Critical value 1.95 What condition for using a z-distribution is met? test statistic (z) 1.8 p-value 0.072 Pick V What is the level of significance? Ex: 0.12 $ What is the null hypothesis Ho? Pick What is the alternative hypothesis Ha? Pick Should Ho be rejected or does Ho fail to be rejected? Pick What conclusion can be drawn from the data? Pick v idence exists to support the claim that the number of customers who visit the site and make a Pick rchase is not 50%. Insufficient Sufficient