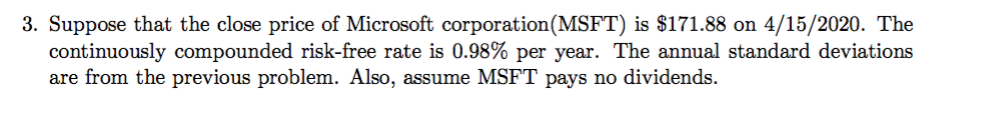
Annual return = 0.1082 , Annual standard deviation = 0.2371

3. Suppose that the close price of Microsoft corporation(MSFT) is $171.88 on 4/15/2020. The continuously compounded risk-free rate is 0.98% per year. The annual standard deviations are from the previous problem. Also, assume MSFT pays no dividends. (a) Lets consider a European put option with a strike price of $ 175.00 expiring on 1/15/2021 and use the annualized standard deviation from problem 2. i. Compute the value of a three-step binomial tree (BT) model. (Divide the investment horizon into three pieces.) ii. Compute the BLACK-SCHOLES (BS) formula, which is given by call option : c= SoN(d1) - Xe="TN(d2) put option : p= Xe-rTN(-da) Soe-TN(-d1) In(So/X) + (r + 02/2)T di = OVT In(S0/X) + (1 - 02/2)T d2= OVT That is, d2 = di -OVT where: T: Time to maturity So : Asset price X: Exercise price r: Continuously compounded risk free rate o : Volatility of continuously compounded return on the stock N(*) : Cumulative Normal Probability iii. For this time, compute the option price with a nine-step binomial tree. iv. Compare all three prices from the previous problems. 3. Suppose that the close price of Microsoft corporation(MSFT) is $171.88 on 4/15/2020. The continuously compounded risk-free rate is 0.98% per year. The annual standard deviations are from the previous problem. Also, assume MSFT pays no dividends. (a) Lets consider a European put option with a strike price of $ 175.00 expiring on 1/15/2021 and use the annualized standard deviation from problem 2. i. Compute the value of a three-step binomial tree (BT) model. (Divide the investment horizon into three pieces.) ii. Compute the BLACK-SCHOLES (BS) formula, which is given by call option : c= SoN(d1) - Xe="TN(d2) put option : p= Xe-rTN(-da) Soe-TN(-d1) In(So/X) + (r + 02/2)T di = OVT In(S0/X) + (1 - 02/2)T d2= OVT That is, d2 = di -OVT where: T: Time to maturity So : Asset price X: Exercise price r: Continuously compounded risk free rate o : Volatility of continuously compounded return on the stock N(*) : Cumulative Normal Probability iii. For this time, compute the option price with a nine-step binomial tree. iv. Compare all three prices from the previous problems