answer all questions with explanation

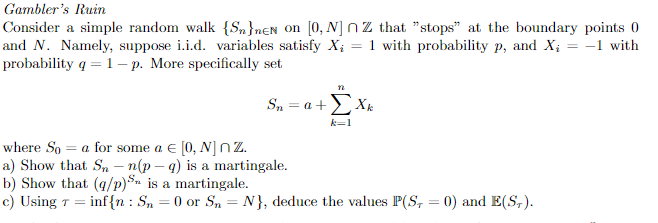
Gambler's Ruin Consider a simple random walk {S)new on [0, N] n Z that "stops" at the boundary points ( and N. Namely, suppose i.i.d. variables satisfy X, = 1 with probability p, and X; = -1 with probability q =1 -p. More specifically set Sn = a+> Xk k-1 where So = a for some a E [0, N]nZ. a) Show that S - n(p - q) is a martingale. b) Show that (q/p)' is a martingale. c) Using T = inf{n : Sn =0 or Sn = N}, deduce the values PP(S, = 0) and E(S.)