Answer number 1 and 2

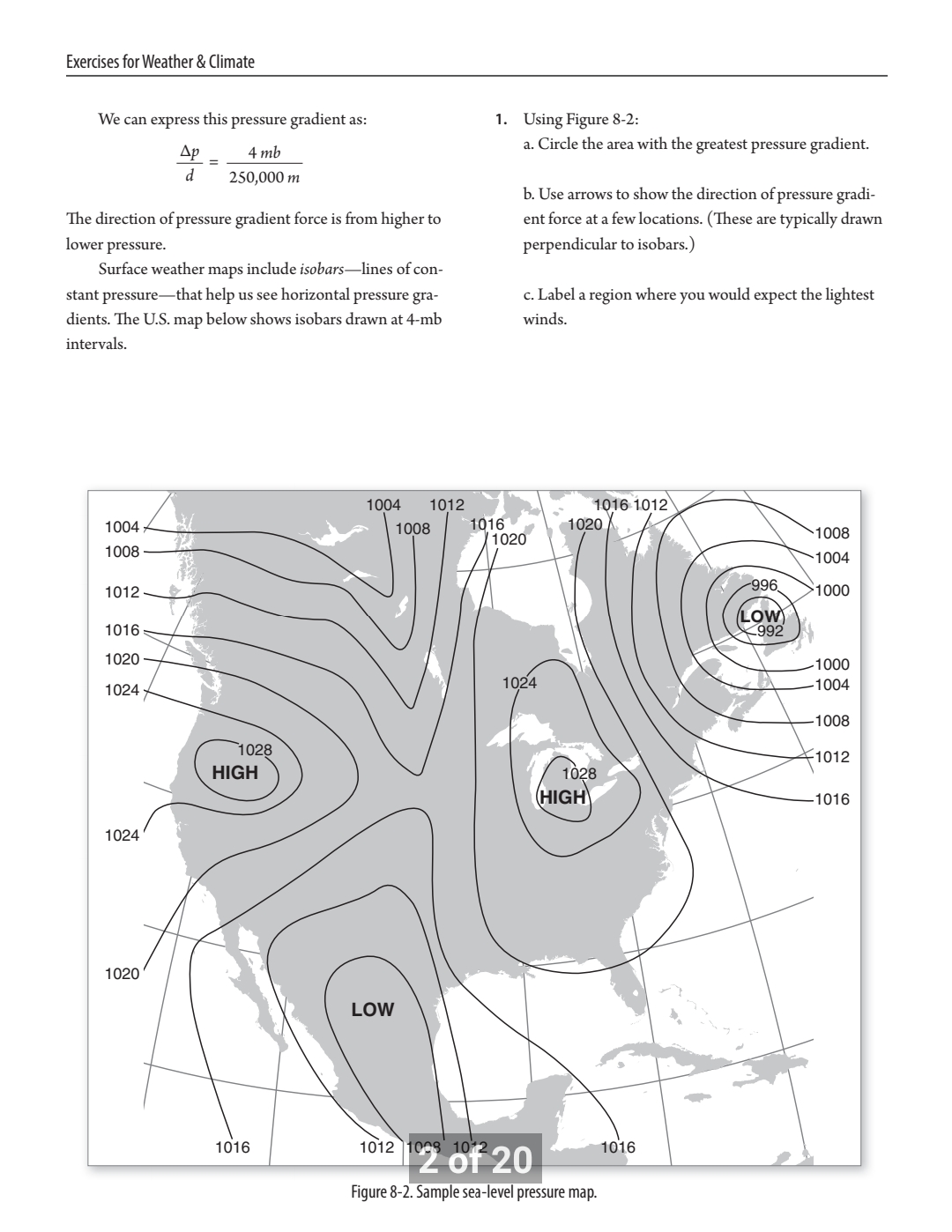
Pressure Gradient Force Horizontal winds are driven by horizontal differ- 160 ences in pressure between two locations. This pressure Station A difference is referred to as a horizontal pressure gradient. The 200 Station B O greater its value, the stronger the wind. Consider stations A and B in Figure 8-1, separated by 250 km.* The pressure 250 km is 1016 mb at station A and 1020 mb at station B-a 4-mb pressure difference over 250 km. Figure 8-1. Pressure gradient. *Note how pressure is depicted on surface weather maps. To decode the values shown, first move the decimal one place to the left (e.g., station A with a value of 160 becomes 16.0). Then preface the number with a "9" or a "10." Since sea level pressure on Earth is generally between 950 and 1050 mb, we can safely assume a pressure of 1016.0 mb at station A and 1020.0 mb at station B.Exercises forWeather 8: Climate We can express this pressure gradient as: The direction of pressure gradient force is from higher to lower pressure. Surface weather maps include isobarslines of con- stant pressurethat help us see horizontal pressure gra- dients. The US. map below shows isobars drawn at 4mb intervals. . Using Figure 3-2: a. Circle the area with the greatest pressure gradient. 1). Use arrows to show the direction of pressure gradi- ent force at a fewlocations. (These are typically drawn perpendicular to isobars.) 4:. Label 9. region where you would expect the lightest winds. g ure 3-2. Sample sea-level pressure map. Lle D ' HLIIIU5|JIIEIIL MUlIUII Optional Exercise: Mathematical Treatment of the Pressure Gradient Force The magnitude of the pressure gradient force is a function of the pressure difference between two points and air density. It can be expressed as: where FPG = pressure gradient force m=unitmass (1kg) p = air density (kg m'3) AP = pressure change (pascals orkg m'l 5'2) :5 = distance (In) Let's consider an example where the pressure 5 km above Little Rock1 Arkansas, is 540 mb and 5 km above St. Louis, Missouri, it is 530 mb. The distance between the two cities is 450 kmJ and the air density at 5 km is approxi- mately 0.75 kg m '3. In order to use the pressure gradient equation, we must use compatible units. We rst convert pressure from millibars to pascals (Pa) , another measure of pressure that has units of kilograms per meter per second squared. (Note that 1 mb = 100 Pa.) In our example the pressure difference above the two cities is 10 mb or 1000I Pa (1000 kg m1 s'z). Thus we have: FPG 1 1,000 kg m1 s2 _ = 0.00296 m 5-2 m 0.75 kg 111-3 450,000 m Newton's second law states that force equals mass times acceleration {F = m o a). In our example we have considered pressure gradient force per unit mass; therefore our result is an acceleration (P + m = :3). Because of the small units shown above, pressure gradient acceleration is often expressed as centimeters per second squared. In this example we have -0.296 cm sec'z. 2. Assuming a sea-level air density of 1.2 kg m'3' calculate the magnitude of the pressure gradient force per unit mass in Figure 8-1