**ANSWER QUESTION 36 AND QUESTION 37**

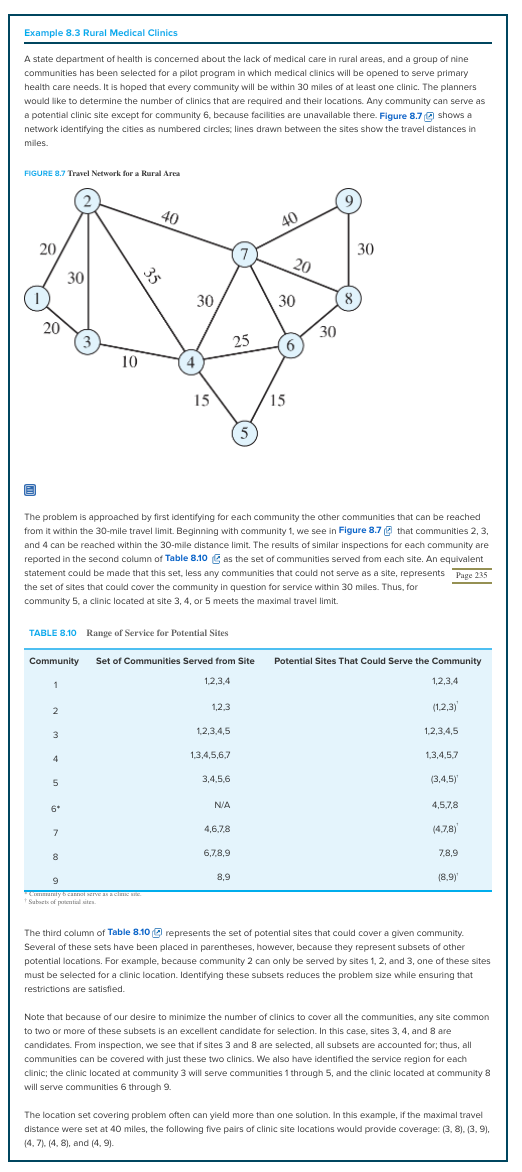
8.10. Recall the rural medical clinics in Example 8.3 and suppose that each community were required to be 25 miles at most from the nearest clinic. How many clinics would be needed, and what would their locations be? Give all possible location solutions. Example 8.3 Rural Medical Clinics A state department of health is concemed about the lack of medical care in rural areas, and a group of nine communities has been selected for a pilot program in which medical clinics will be opened to serve primary health care needs. It is hoped that every community will be within 30 miles of at least one clinic. The planners would like to determine the number of clinics that are required and their locations. Any community can serve as a potential clinic site except for community 6. because facilities are unavailable there. Figure 8.7 shows a network identifying the cities as numbered circles, lines drawn between the sites show the travel distances in miles FIGURE 8.7 Travel Network for a Rural Area a 40 40 20 7 30 20 35 30 1 20 30 30 8 30 3 25 6 10 15 15 5 The problem is approached by first identifying for each community the other communities that can be reached from it within the 30-mile travel limit. Beginning with community 1, we see in Figure 8.7 that communities 2, 3, and 4 can be reached within the 30-mile distance limit. The results of similar inspections for each community are reported in the second column of Table 8.10 as the set of communities served from each site. An equivalent statement could be made that this set, less any communities that could not serve as a site, represents Page 235 the set of sites that could cover the community in question for service within 30 miles. Thus, for community 5. a clinic located at site 3, 4, or 5 meets the maximal travel limit. TABLE 8.10 Range of service for Potential Sites Community Set of Communities Served from Site Potential Sites That Could Serve the Community 1 1,2,3,4 1,2,3,4 2 1,2,3 (1,2,3) 3 12,3,4,5 1,2,3,4,5 1,3,4,5,6,7 4 1,3,4,5,7 5 3,4,5,6 (3,4,5) 6 NA 4,5,7,8 7 4,6,7,8 (4.7,8) 8 6,7,8,9 7,8,9 8.9 (8,9) 9 . Sabot The third column of Table 8.10 @ represents the set of potential sites that could cover a given community a . Several of these sets have been placed in parentheses, however, because they represent subsets of other potential locations. For example, because community 2 can only be served by sites 1, 2, and 3, one of these sites must be selected for a clinic location. Identifying these subsets reduces the problem size while ensuring that restrictions are satisfied. Note that because of our desire to minimize the number of clinics to cover all the communities, any site common to two or more of these subsets is an excellent candidate for selection. In this case, sites 3, 4, and 8 are candidates. From inspection, we see that if sites 3 and 8 are selected, all subsets are accounted for; thus, all communities can be covered with just these two clinics. We also have identified the service region for each clinicthe clinic located at community 3 will serve communities through 5, and the clinic located at community 8 will serve communities 6 through 9. The location set covering problem often can yield more than one solution. In this example, if the maximal travel distance were set at 40 miles, the following five pairs of clinic site locations would provide coverage: (3.8). (3.9), 14,7). (4.8), and (4.9). Problem 8.10 Use your results for homework problem 8.10 to answer the following questions. Question 36 (2 points) Listen How many clinics would be needed? 1 O2 3 4 More than 4 Question 37 (2 points) Listen Which of the following combinations are part of the possible location solution? Check all that apply. 1 or 2 1 or 2 or 4 4 or 5 3 or 4 or 5 7 or 8 6 or 8 or 8 8 09 8.10. Recall the rural medical clinics in Example 8.3 and suppose that each community were required to be 25 miles at most from the nearest clinic. How many clinics would be needed, and what would their locations be? Give all possible location solutions. Example 8.3 Rural Medical Clinics A state department of health is concemed about the lack of medical care in rural areas, and a group of nine communities has been selected for a pilot program in which medical clinics will be opened to serve primary health care needs. It is hoped that every community will be within 30 miles of at least one clinic. The planners would like to determine the number of clinics that are required and their locations. Any community can serve as a potential clinic site except for community 6. because facilities are unavailable there. Figure 8.7 shows a network identifying the cities as numbered circles, lines drawn between the sites show the travel distances in miles FIGURE 8.7 Travel Network for a Rural Area a 40 40 20 7 30 20 35 30 1 20 30 30 8 30 3 25 6 10 15 15 5 The problem is approached by first identifying for each community the other communities that can be reached from it within the 30-mile travel limit. Beginning with community 1, we see in Figure 8.7 that communities 2, 3, and 4 can be reached within the 30-mile distance limit. The results of similar inspections for each community are reported in the second column of Table 8.10 as the set of communities served from each site. An equivalent statement could be made that this set, less any communities that could not serve as a site, represents Page 235 the set of sites that could cover the community in question for service within 30 miles. Thus, for community 5. a clinic located at site 3, 4, or 5 meets the maximal travel limit. TABLE 8.10 Range of service for Potential Sites Community Set of Communities Served from Site Potential Sites That Could Serve the Community 1 1,2,3,4 1,2,3,4 2 1,2,3 (1,2,3) 3 12,3,4,5 1,2,3,4,5 1,3,4,5,6,7 4 1,3,4,5,7 5 3,4,5,6 (3,4,5) 6 NA 4,5,7,8 7 4,6,7,8 (4.7,8) 8 6,7,8,9 7,8,9 8.9 (8,9) 9 . Sabot The third column of Table 8.10 @ represents the set of potential sites that could cover a given community a . Several of these sets have been placed in parentheses, however, because they represent subsets of other potential locations. For example, because community 2 can only be served by sites 1, 2, and 3, one of these sites must be selected for a clinic location. Identifying these subsets reduces the problem size while ensuring that restrictions are satisfied. Note that because of our desire to minimize the number of clinics to cover all the communities, any site common to two or more of these subsets is an excellent candidate for selection. In this case, sites 3, 4, and 8 are candidates. From inspection, we see that if sites 3 and 8 are selected, all subsets are accounted for; thus, all communities can be covered with just these two clinics. We also have identified the service region for each clinicthe clinic located at community 3 will serve communities through 5, and the clinic located at community 8 will serve communities 6 through 9. The location set covering problem often can yield more than one solution. In this example, if the maximal travel distance were set at 40 miles, the following five pairs of clinic site locations would provide coverage: (3.8). (3.9), 14,7). (4.8), and (4.9). Problem 8.10 Use your results for homework problem 8.10 to answer the following questions. Question 36 (2 points) Listen How many clinics would be needed? 1 O2 3 4 More than 4 Question 37 (2 points) Listen Which of the following combinations are part of the possible location solution? Check all that apply. 1 or 2 1 or 2 or 4 4 or 5 3 or 4 or 5 7 or 8 6 or 8 or 8 8 09