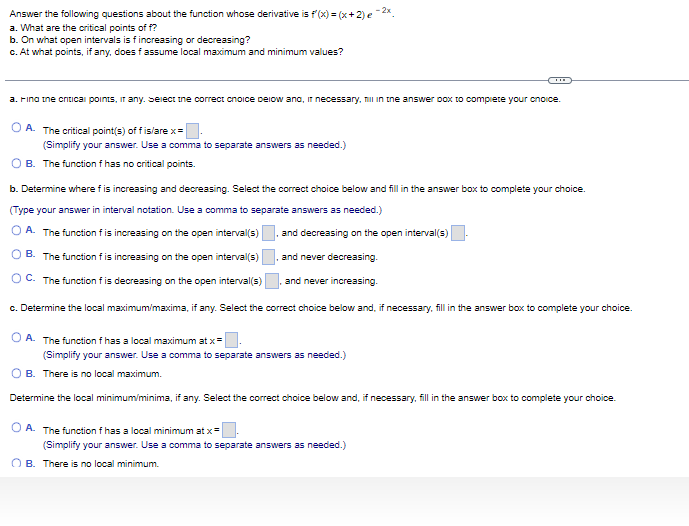
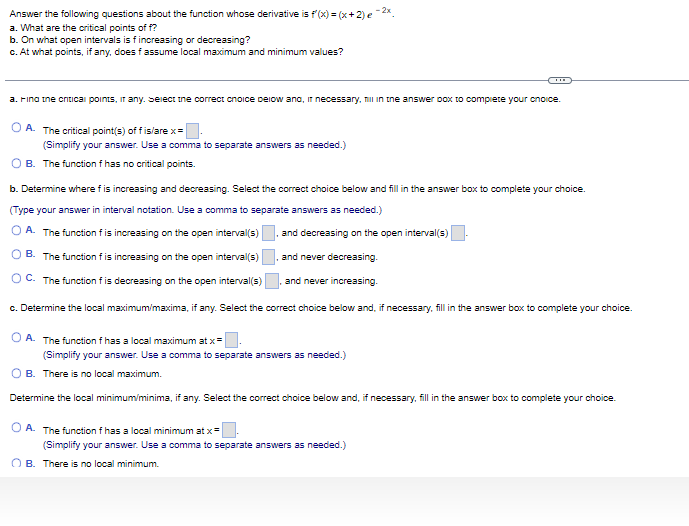
Answer the following questions about the function whose derivative is f(x) = (x+2) e -2x. a. What are the critical points of f? b. On what open intervals is f increasing or decreasing? C. At what points, if any, does f assume local maximum and minimum values? a. Find the critical points, IT any. Select ine correct choice below and, If necessary, fill In the answer box to complete your choice. O A. The critical point(s) of fis/are x= (Simplify your answer. Use a comma to separate answers as needed.) O B. The function fhas no critical points. b. Determine where f is increasing and decreasing. Select the correct choice below and fill in the answer box to complete your choice. (Type your answer in interval notation. Use a comma to separate answers as needed.) A. The function f is increasing on the open interval(s) , and decreasing on the open interval(s) O B. The function f is increasing on the open interval(s) , and never decreasing. O C. The function f is decreasing on the open interval(s) , and never increasing. c. Determine the local maximum/maxima, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The function fhas a local maximum at x = (Simplify your answer. Use a comma to separate answers as needed.) O B. There is no local maximum. Determine the local minimum/minima, if any. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. The function f has a local minimum at x = (Simplify your answer. Use a comma to separate answers as needed.) O B. There is no local minimum