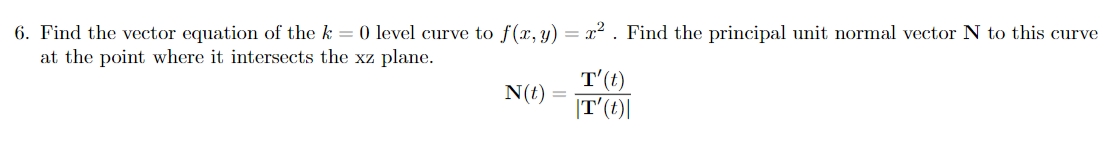
Answer the following questions, be SPECIFIC!

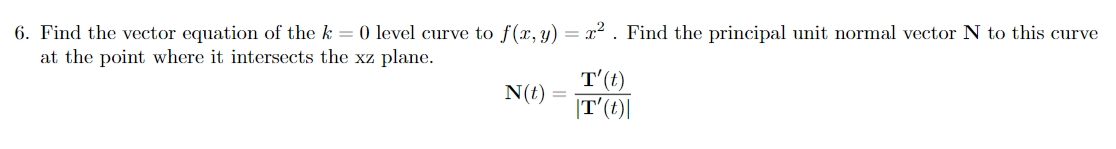
16. Let S be a. sphere centered at the origin containing point P[2, -3, 6). (a) Find the equation of the tangent plane to the sphere at the specied point. (b) Find the coordinate at which the normal line to the sphere at the given point intercepts the xy plane. 12. Find the tangent line to the vector valued function given by: 7(t) = (oos[t), sin{t), t) at the point t = 3\" 13. Suppose the velocity of a particle is described by: 5'6) = (1 2t, 2t, 0) and the position 71(0) = {0, , '2) is known. (a) Find the position function FE) (b) Find the acceleration vector RR) (c) Find the minimum speed of the particle and the time it occurs. 14. Let ?(t) = (3cos(t),3sin(t),0) (3) Find T, N and B (the unit tangential, unit normal and unit binormal vectors to ?(t)) (b) Compute the arclength described by ?(t) for the segment drawn by D g t g 5% 6. Find the vector equation of the k = 0 level curve to f(:r:, y) = 1'2 . Find the principal unit normal vector N to this curve at the point where it intersects the X2 plane. _ M) N\") ' IT'(t)|