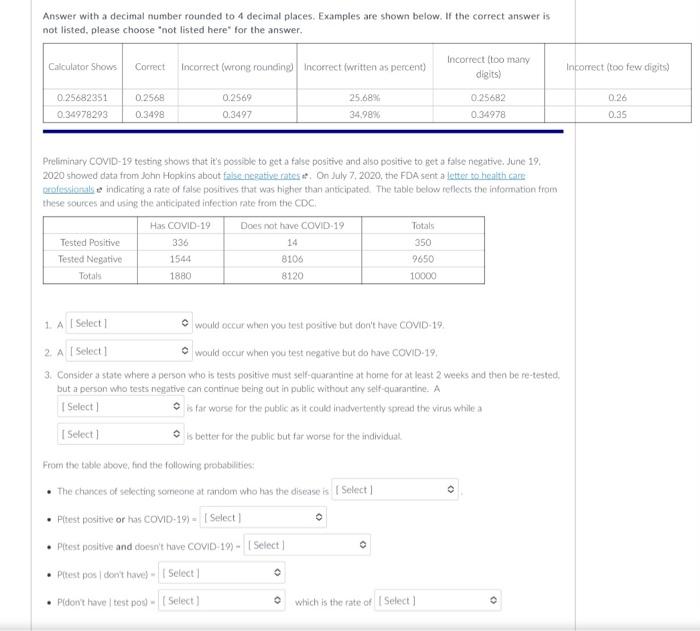
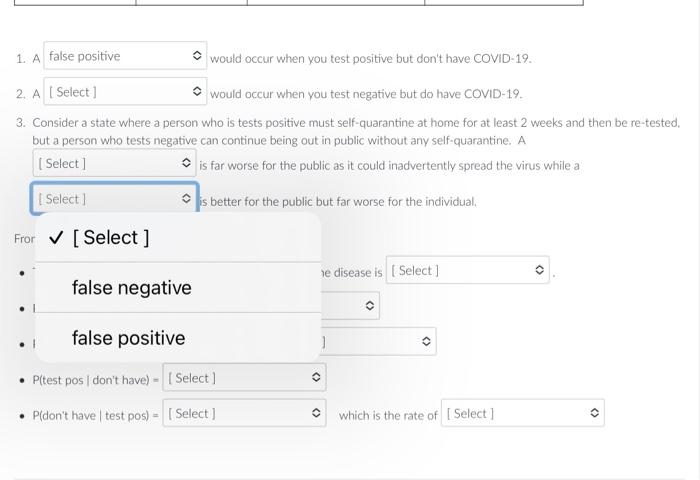
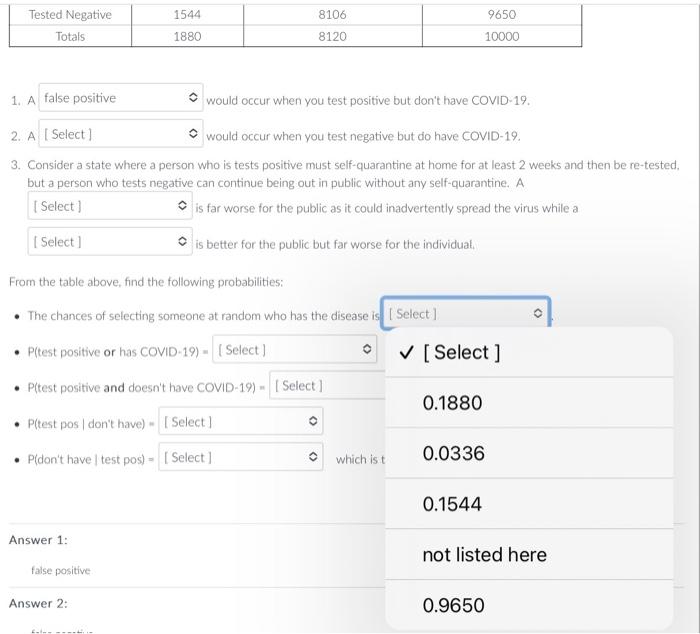
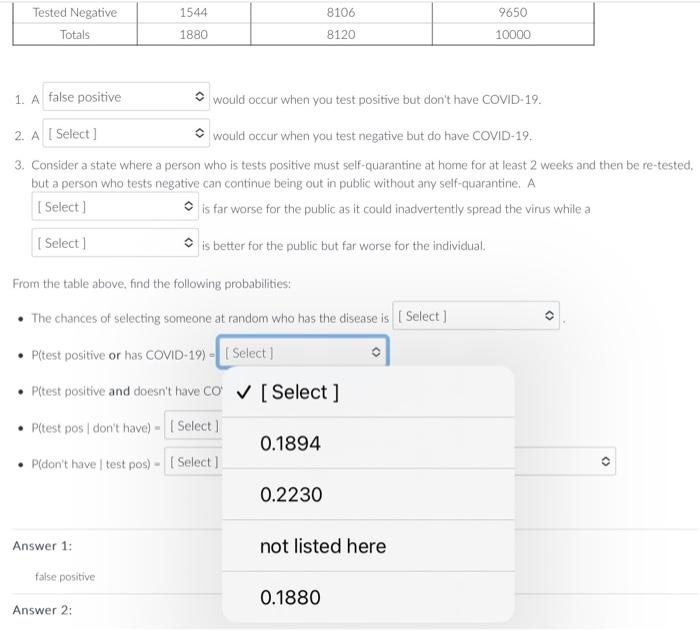
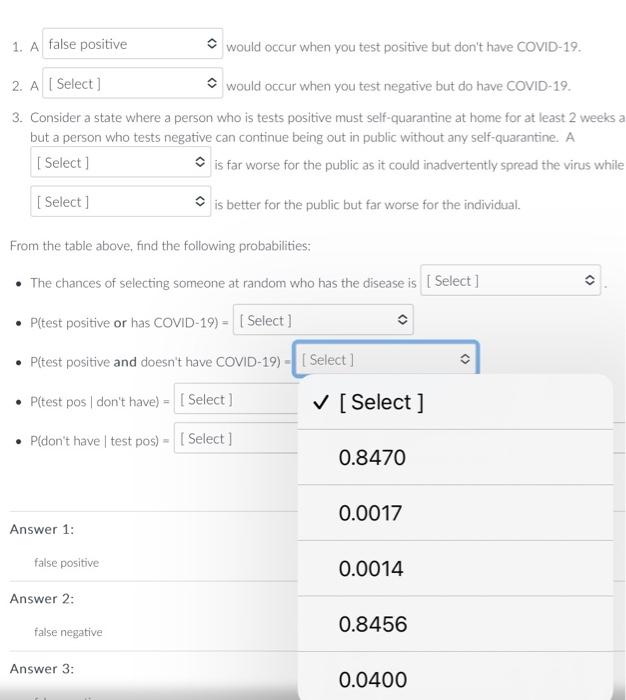
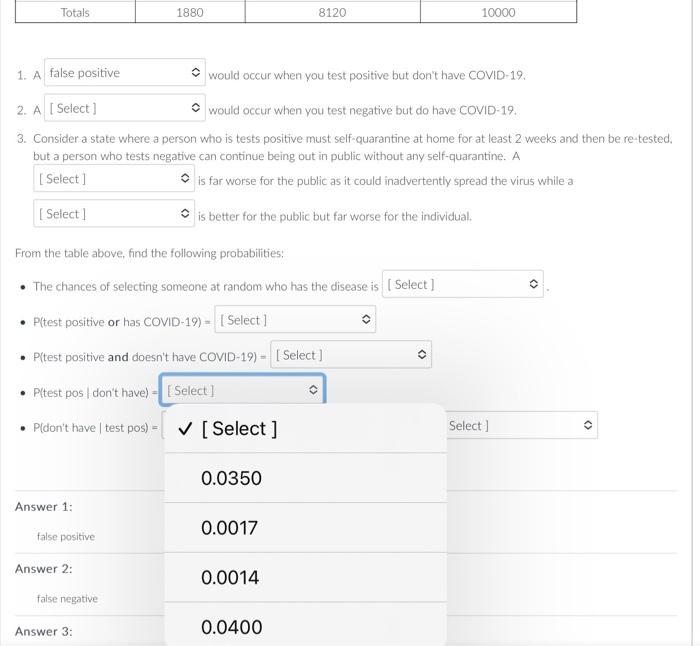
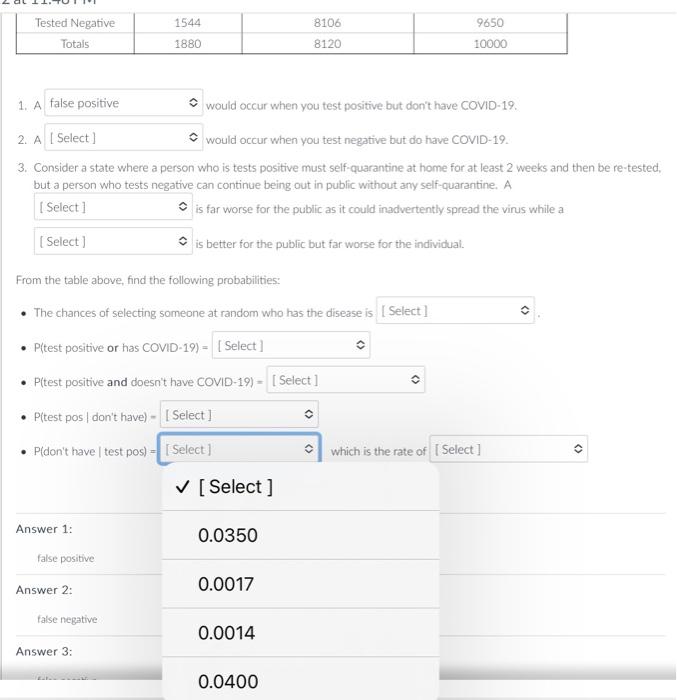
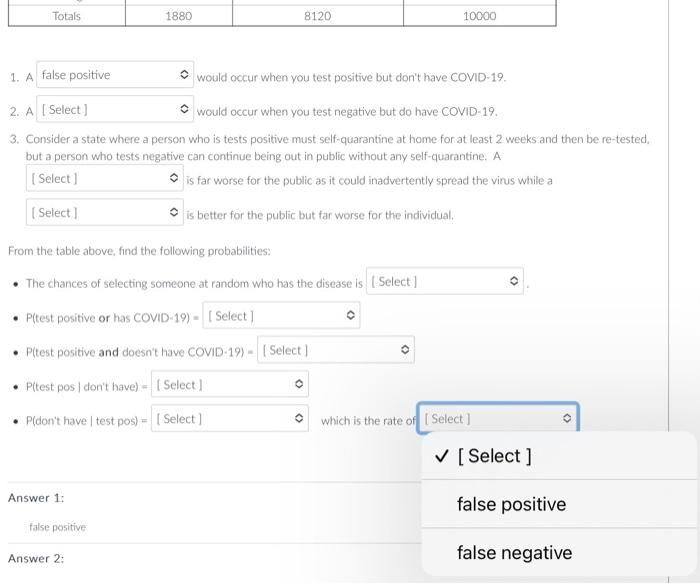
Question: Answer with a decimal number rounded to 4 decimal places. Examples are shown below. If the correct answer is not listed. please choose not listed
Answer with a decimal number rounded to 4 decimal places. Examples are shown below. If the correct answer is not listed. please choose "not listed here" for the answer. Preliminary COVID-19 testine shows that it's possible to get a false positive and also positive to get a false negative. June 19 , 2020 showed data from lohn Hopkins about false negatisu rates a*, On July 7,2020 , the FDA sent a lettet ia health sare erofessionals e indicating a rate of false posifives that was highe than anticipated. The table below reflects the information from these sources and using the anticipated infection rate from the CDC: 1 A would occur when you test positive but don't hawe COMID-19. 2. A would occur when you test negative but do have COVID-19, 3. Consider a state where a) person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tested, but a person who tests negative can continue being out in public without amy self-quarantirne. A E far worse for the public as it coulef inattvertertly spread the virus while a is better for the public but far worse for the individual. From the table above, fund the following probabilities: - The chances of selecting sorncone at random who has the disease is - Pitest positive or has COVID-19) = - P(test positive and docsn't have COVID-19) = - P(test pos ( dont have) = - Pidont have 1 test posi) = which is the rate of Preliminary COVID-19 testing shows that it's possible to get a false positive and also positive to get a false negative. June 19. 2020 showed data from John Hopkins about false negative rates w. On July 7, 2020, the FDA sent a letter to health care professionals c indicating a rate of false positives that was higher than anticipated. The table below reflects the information from these sources and using the anticipated infection rate from the CDC. 1. A would occur when you test positive but don't have COVID-19. as it could inadvertently spread the virus while a false negative far worse for the individual. From : false positive - P(t true positive disease is - P(test positive and doesn't have COVID-19) = - P(test pos / don't have )= - P (don't have test pos) = which is the rate of Preliminary COVID-19 testing shows that it's possible to get a false positive and also positive to get a false negative. June 19. 2020 showed data from John Hopkins about false negative rates s*. On July 7. 2020, the FDA sent a letter to health care professionals in indicating a rate of false positives that was higher than anticipated. The table below reflects the information from these sources and using the anticipated infection rate from the CDC. 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tested, but a person who tests negative can continue being out in public without any self-quarantine, A is far worse for the public as it could inadvertently spread the virus while a [Select ] iut far worse for the individual. Fror false positive le disease is false negative - P(test positive and doesn't have COVID-19) = - P(test pos don't have) = - P(don't have | test pos) = which is the rate of 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tested. but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while a is better for the public but far worse for the individual. Fror [ Select ] false negative le disease is - I - false positive - P(test pos don't have) = - P( don't have test pos) = which is the rate of 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tested. but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while a is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P(test positive or has COVID-19) = [ Select ] - P(test positive and doesn't have COVID-19) = 0.1880 - P( test pos 1 don't have) = - P(don't have test pos) = which is 0.0336 Answer 1: not listed here false positive 0.1544 Answer? 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tes but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while a is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P(test positive or has COVID-19) = - P(test positive and doesn't have co' [Select] Answer1:falsepositivenotlistedhere0.1880 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks a but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P( test positive or has COVID-19) = - P(test positive and doesn't have COVID-19) = 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-test but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while a is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P(test positive or has COVID-19) = - P(test positive and doesn't have COVID-19) = - P(test pos (don't have) = - P(don't have test pos) = 0.0350 Answer 1: 0.0017 Answer 2: 0.0014 false negative 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-t, but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the vinus while a is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P(test positive or has COVID-19) = - P(test positive and doesn't have COVID-19) = - P(test pos 1 don't have) = - P(don't have test pos) = which is the rate of [Select ] Answer 1: 0.0350 false positive Answer 2: 0.0017 false negative 0.0014 Answer 3: 1. A would occur when you test positive but don't have COVID-19. 2. A would occur when you test negative but do have COVID-19. 3. Consider a state where a person who is tests positive must self-quarantine at home for at least 2 weeks and then be re-tested, but a person who tests negative can continue being out in public without any self-quarantine. A is far worse for the public as it could inadvertently spread the virus while a is better for the public but far worse for the individual. From the table above, find the following probabilities: - The chances of selecting someone at random who has the disease is - P(test positive or has COVID-19) = - P(test positive and doesn't have COVID-19) = - P( test pos don't have )= - P (don't have test pos) = which is the rate of