Any code needs to be in R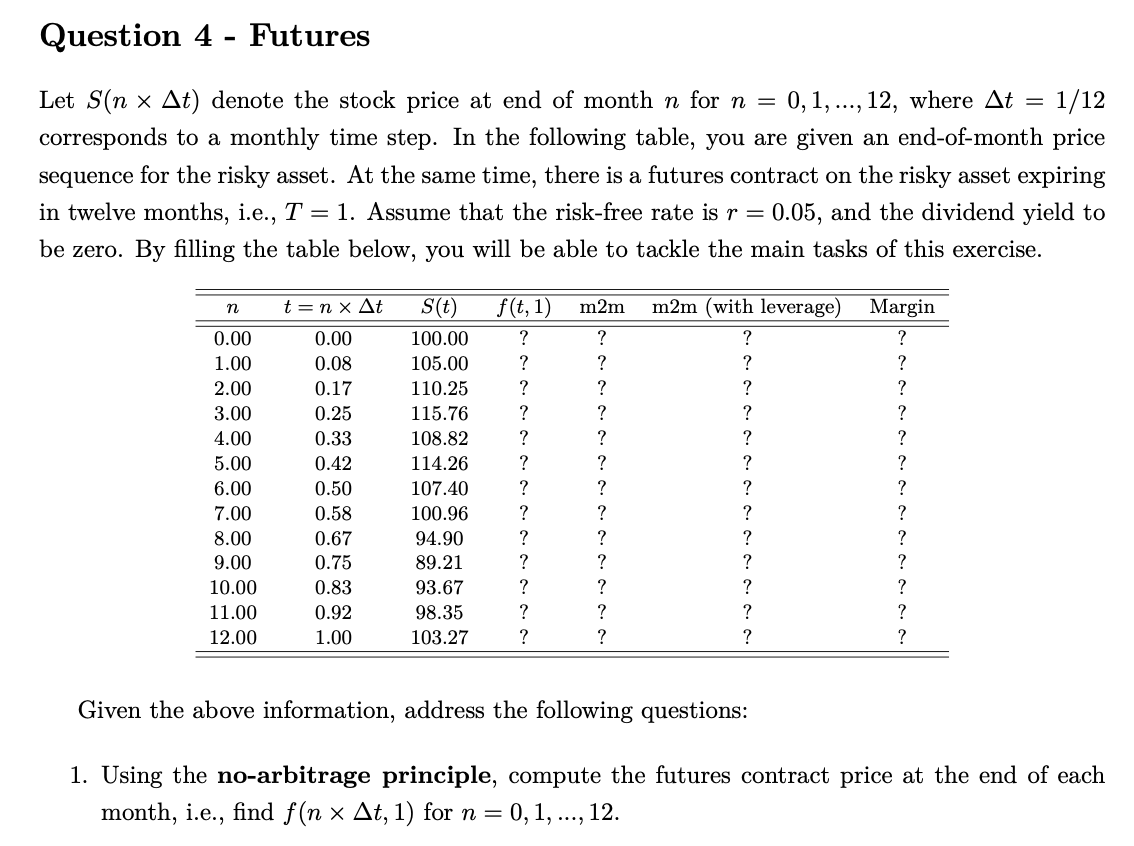

Question 4 - Futures Let S(n x At) denote the stock price at end of month n for n = 0,1, ..., 12, where At = - 1/12 corresponds to a monthly time step. In the following table, you are given an end-of-month price sequence for the risky asset. At the same time, there is a futures contract on the risky asset expiring in twelve months, i.e., T = 1. Assume that the risk-free rate is r = 0.05, and the dividend yield to be zero. By filling the table below, you will be able to tackle the main tasks of this exercise. n t=nx At m2m 0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 0.00 0.08 0.17 0.25 0.33 0.42 0.50 0.58 0.67 0.75 0.83 0.92 1.00 S(t) 100.00 105.00 110.25 115.76 108.82 114.26 107.40 100.96 94.90 89.21 93.67 98.35 103.27 f(t, 1) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? m2m (with leverage) ? ? ? ? ? ? ? ? ? ? ? ? ? Margin ? ? ? ? ? ? ? ? ? ? ? ? ? Given the above information, address the following questions: 1. Using the no-arbitrage principle, compute the futures contract price at the end of each month, i.e., find f(n * At, 1) for n= 0,1, ..., 12. Question 4 - Futures Let S(n x At) denote the stock price at end of month n for n = 0,1, ..., 12, where At = - 1/12 corresponds to a monthly time step. In the following table, you are given an end-of-month price sequence for the risky asset. At the same time, there is a futures contract on the risky asset expiring in twelve months, i.e., T = 1. Assume that the risk-free rate is r = 0.05, and the dividend yield to be zero. By filling the table below, you will be able to tackle the main tasks of this exercise. n t=nx At m2m 0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 0.00 0.08 0.17 0.25 0.33 0.42 0.50 0.58 0.67 0.75 0.83 0.92 1.00 S(t) 100.00 105.00 110.25 115.76 108.82 114.26 107.40 100.96 94.90 89.21 93.67 98.35 103.27 f(t, 1) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? m2m (with leverage) ? ? ? ? ? ? ? ? ? ? ? ? ? Margin ? ? ? ? ? ? ? ? ? ? ? ? ? Given the above information, address the following questions: 1. Using the no-arbitrage principle, compute the futures contract price at the end of each month, i.e., find f(n * At, 1) for n= 0,1, ..., 12