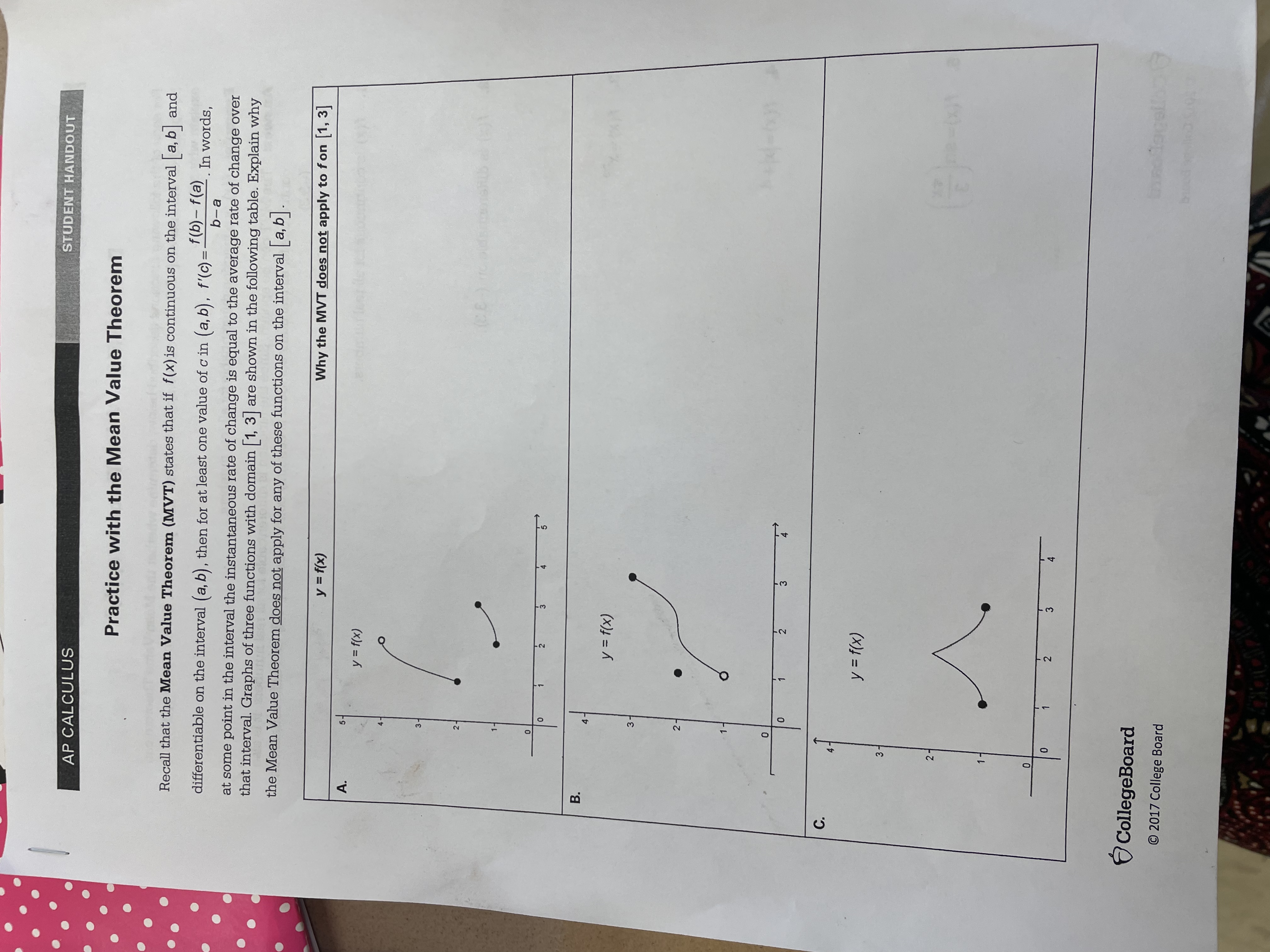
Question: AP CALCULUS STUDENT HANDOUT Practice with the Mean Value Theorem Recall that the Mean Value Theorem (MVT) states that if f(x) is continuous on the

![on the interval [a, b] and differentiable on the interval (a, b)](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/670968bc651ee_883670968bbc7f06.jpg)
AP CALCULUS STUDENT HANDOUT Practice with the Mean Value Theorem Recall that the Mean Value Theorem (MVT) states that if f(x) is continuous on the interval [a, b] and differentiable on the interval (a, b) , then for at least one value of c in (a, b), f'(c) =_)(). In words, b - a at some point in the interval the instantaneous rate of change is equal to the average rate of change over that interval. Graphs of three functions with domain [1, 3] are shown in the following table. Explain why the Mean Value Theorem does not apply for any of these functions on the interval [a, b]. y = f ( x ) Why the MVT does not apply to fon [1, 3] A. y = f ( x ) 0 2 3 4 B. 4 - y = f ( x ) 3 - 2 1 - 0 2 3 C. y = f (x ) 3 - N 10 2 3 CollegeBoard 2017 College Boardestion 2 antiable. A graph of the net graph to ans er these questions: which of any ection points of g(x)? AP CALCULUS 6. f(x) = tan #x 7. 1(x )-x4 +3, x51 2x +2 x> 1 Graph of y = 91x), thec (This graph has a horizontal t1043 SF s concurity STUDENT HANDOUT Let's look at the regula caltaron. DuoSJOd S Concavity and Inflection Notice that the 'noso these peal nok waym post i paau now you suedw Write the ys!Ibu3 meaning of sentences in Use the above c and that the action was lotice that the endings underlined part) of the v using the Conjugate these verbs verb chart: and that f(x) = (x - 1)2 (x - 2). Which x-values have f"(x) =0? What action points of ?? derivative of g, that is, y = g'(x), STUDENT HANDOUT -values have g"(x) =0, and what AP CALCULUS Does the Mean Value Theorem apply? For each of the following functions described below, determine whether the Mean Value Theorem can be applied on the interval [-3,3) . If it can be applied, explain how you know. If it cannot be applied, explain why not. 1 Example: f(x) is a function differentiable for all real numbers. Answer: The MVT can be applied. Since the function is differentiable for all real numbers, it is also 2 continuous for all real numbers. So it is certainly continuous on [-3,3] and differentiable on 4 (-3, 3). 1. f(x) is continuous for all real numbers. f g(x) x =-2.) 2. f(x) is differentiable on (-3, 3). 3. f ( x ) = x 23 4. f ( x) = /x/+ 4 5 . f ( x ) = sin * x (3 CollegeBoard 2017 College Board
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


