Question: Applications of the Derivative 5. Let g be the function given by g(x) = x4 - 4x3 + 6x2 - 4x + k, where k

Applications of the Derivative

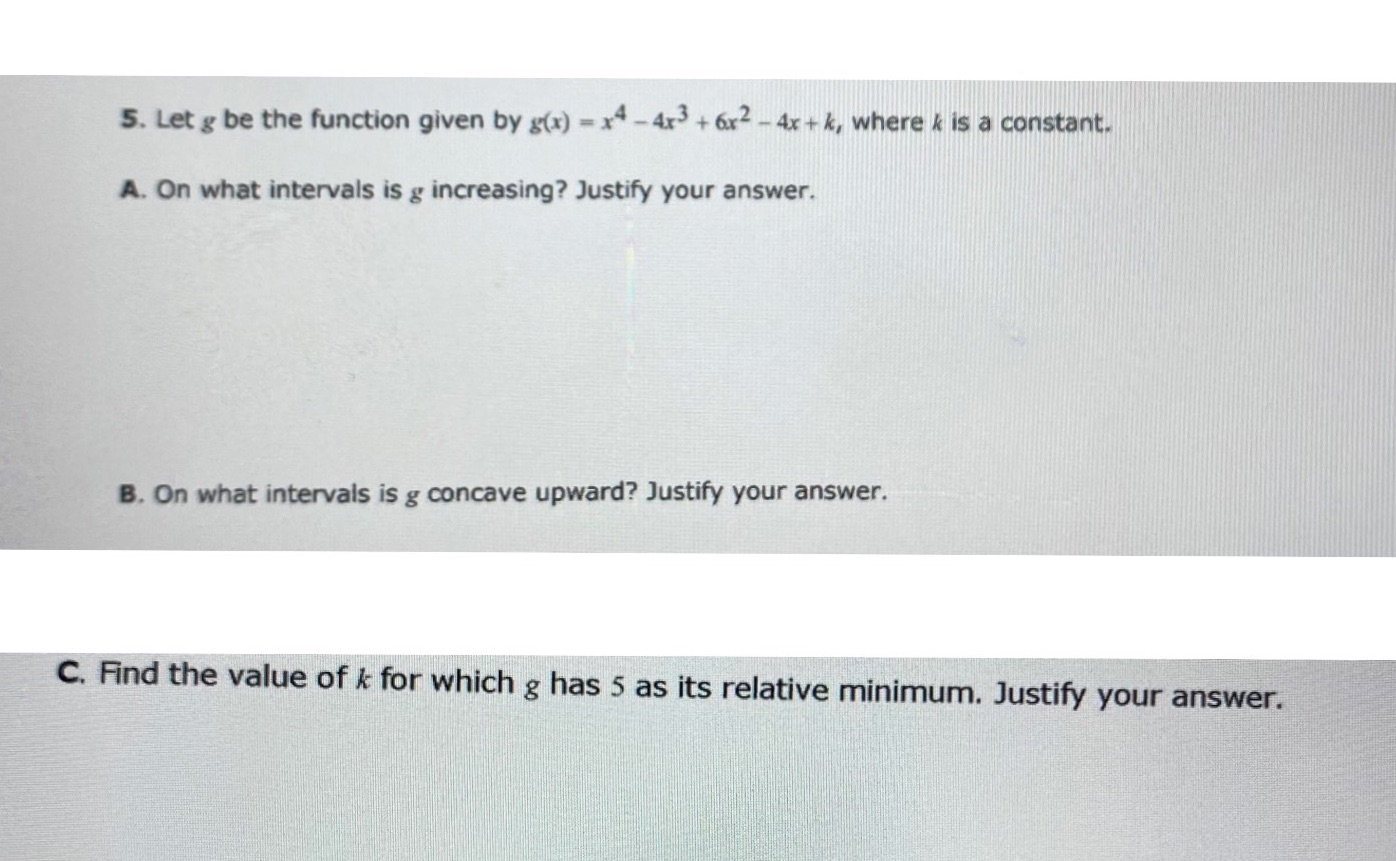
5. Let g be the function given by g(x) = x4 - 4x3 + 6x2 - 4x + k, where k is a constant. A. On what intervals is g increasing? Justify your answer. B. On what intervals is g concave upward? Justify your answer. C. Find the value of & for which g has 5 as its relative minimum. Justify your

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

B. Smitty Smith is a project manager for a large consumer electronics corporation. Although she has been with the company only four years, she has demonstrated an uncanny ability to bring projects in...

5. Let g be the function given by g(x) =x4 - 4x3 + 6x - 4x+ k, where k is a constant. A. On what intervals is g increasing? Justify your answer. g'(x) >0 for increasing function g(x) 4x-12x+12x-4 >0...

Directions Complete the following 2 FRQ problems They each have 4 parts a d associated with them and each are out of 9 points total 1 Particle A is moving along the x axis Let f be the continuous...

The rate at which gasoline flows out of a tank, in gallons per hour, is given by a differentiable function G of time t. The table below shows the rate as measured every 4 hours for a 24-hour period:...

Please show all work In (4+h)-in4 13. lim h-0 h (A) O (B) (C)1 (De (E) DNE 14. Let g be the function given by g(x) = xlehr, where k is a constant. For what value of k does g have a critical point at...

answer the following 5) If g is the function given by g(x) = 4x3 + 2x2 - 70x + 5, on which of the following intervals is g decreasing? a. (-00, -10) and (7, 00) b. (-00, -7) and (10, co) (-00, -10)...

Lesson 05.09 Analytical Applications of Differentiation Discussion-Based Assessment Assigned Problems 101234EBTBE 1. The gure above shows the graph of f', the derivative of the function f on the...

Need some help with these problems.Ignore the little piece of the graph at the topthanks in advance!! 18. Identify the open interval(s) on which the function f(x) = x - x-12 is increasing. (A) (-00,...

Lesson 05.11 Analytical Applications of Differentiation Discussion-Based Assessment Assigned Problems 1. The figure above shows the graph of f', the derivative of the function f on the closed...

1. (01.09 HC) Let g be the function given by \"KPH. 6x2 +x2 Part A: Does the graph ofg have a vertical asymptote? If so, write ii: equation and describe the behavior of the graph ofg as it approaches...

Differentiation: Composite, Implicit, and Inverse Functions Practice Exam Questions Question 1 [3.01] Given g(x) = (e"' 2)3, nd g'(x). Question 2 [3.01] X f(X) 3' '(X) 900 9'00 -3 0 -2 2 -1 0 -6 5 -3...

dSuppose that at the end of 2017 Jimenez decided to adopt the revaluation model for its land and buildings Prepare all required JEs using the following accounts as necessary OCI Gain Revaluations OCI...

On May 10, Paige Corporation issues 2,500 shares of $5 par value common stock for cash at $13 per share. Journalize the issuance of the stock.

At _ _ _ _ _ age, children appear to be able to use some self - regulation strategies. Option A 8 months Option B 4 months Option C 2 months Option D 6 months

A function vis called a conjugate harmonic function for a harmonic function u, whenever: Select one: O vis analytic O uis analytic O f=u +ivis analytic O f=u- ivis analytic

Presented below are unrelated cases involving investments in debt securities: Case 1: A company owns another firm's debt securities in the form of bonds. The bonds were acquired at a discount and are...

The actual demand (in units) and the forecasted demand for a product in the past 4 months were shown below. Month Demand (u) 296 Forecast (u) 217 February March 264 216 April 272 337 May 263 250 Find...

8. Based on a strategy that is used at your workplace, find information that goes against this strategy.

1. Provide new information that contains more than 59 items, depending on the recipients capacity.

3. Give away need to know information and you will get back information that you find useful.