Apply this in areas marked with xxx in given code:

BinarySearchTree.Java

BinarySearchTree.Java

package bst;

import java.util.LinkedList;
import java.util.Queue;
import java.util.*;

public class BinarySearchTree {

private static class BSTNode{
 private int data;
 private int level; // the level of the tree where the node is at

 private BSTNode leftChild;
 private BSTNode rightChild;
 
 public BSTNode(int data) {
  this.data = data;
 }
 
 public String toString() {
  return data+"";
 }
}

private BSTNode root;

public BinarySearchTree(int data) {
 root = new BSTNode(data);
}

public void insert(int data) {
 root = recursiveInsert(root,data);
}

private BSTNode recursiveInsert(BSTNode node, int data) {
 if(node == null) {
  return new BSTNode(data);
 }
 else if(data   node.leftChild = recursiveInsert(node.leftChild,data);
 }
 else if(data > node.data) {
  node.rightChild = recursiveInsert(node.rightChild,data);
 }
 return node;
}

public void delete(int data) {
 root = recursiveDelete(root,data);
}

private BSTNode recursiveDelete(BSTNode node,int data){
 if(node == null) {
  return node;
 }
 else {
 if(data   node.leftChild = recursiveDelete(node.leftChild,data);
 }
 else if(data > node.data) {
  node.rightChild = recursiveDelete(node.rightChild,data);
 }
 else {//we found the node to delete
  if(node.leftChild==null && node.rightChild == null) {
   return null;
  }
  else if(node.leftChild == null) {
   return node.rightChild;
  }
  else if(node.rightChild == null) {
   return node.leftChild;
  }
  else {//Still need to handle the case with two children
   BSTNode predecessor = getMax(node.leftChild);
   int d = predecessor.data;
   node.data = d;//update data at node
   //remove predecessor node
   node.leftChild = recursiveDelete(node.leftChild,d);
  }
 }
 return node;
 }
}

//assumes root is not null
public BSTNode getMax(BSTNode root){
 while(root.rightChild!= null) {
  root = root.rightChild;
 }
 return root;
}

//assumes root is not null
public BSTNode getMin(BSTNode root){
 while(root.leftChild!=null) {
  root = root.leftChild;
 }
 return root;
}

public boolean contains(int data) {
 if(find(data) == null) {return false;}
 else {return true;}
}

public BSTNode find(int key) {
 return recursiveFind(root,key);
}

private BSTNode recursiveFind(BSTNode node,int key) {
 //base case, made it to the end or I found it
 if(node == null || key == node.data) {
  return node;
 }
 if(key   return recursiveFind(node.leftChild,key);
 }
 else {
  return recursiveFind(node.rightChild,key);
 }
 
}

//Print the tree in an preorder fashion
//Print the current node first and then recurse on the children
public void preOrder() {
 System.out.print ( "  Pre-order tree traversal: " );
 if ( root!=null ) {
           ArrayList nodes = collectNodesByPreOrder();
           System.out.println ( nodes );
 }
}

   //Traverse the tree in an preorder fashion
   //collect the current node first and then recurse on the children
   public ArrayList  collectNodesByPreOrder() {
 ArrayList nodes = new ArrayList ();
       collectNodesByPreOrderRecurse(root, nodes);
 return nodes;
   }

public void collectNodesByPreOrderRecurse(BSTNode node, ArrayList nodes) {
 // xxx to be finished ...

}
 

//Traverse the tree in an inorder fashion
//Recursively print the left side of the current node, then the current node,
//then recursively print the right side of current node
//For a bst this will print the values in sorted order from smallest to largest
public void inOrder() {
 System.out.print ( "   In-order tree traversal: " );
 ArrayList  nodes = collectNodesByInOrder();
 System.out.println ( nodes );
}

public ArrayList  collectNodesByInOrder() {
 // xxx to be finished ...
}

public void collectNodesByInOrder(BSTNode node, ArrayList nodes) {
 // xxx to be finished ...
}

//Traverse the tree in an postorder fashion
//Recurse on the children and then print the value in the current node
public void postOrder() {
 System.out.print ( " Post-order tree traversal: " );
 ArrayList nodes = collectNodesByPostOrder( ) ;
 System.out.println ( nodes );
}
public ArrayList collectNodesByPostOrder( ) {
 // xxx to be finished ...
}

public void collectNodesByPostOrder(BSTNode node, ArrayList nodes) {
 // xxx to be finished ...
}
 

//Traverse the tree in an level order fashion
//Print the current node, then the two children, then their children, ...
public void levelOrder() {
 System.out.print ( "Level-order tree traversal: " );
 ArrayList  nodes = collectNodesByLevelOrder() ;
 System.out.println ( nodes);
   }
public ArrayList  collectNodesByLevelOrder() {

 ArrayList  nodes = new ArrayList  ();
 Queue queue = new LinkedList();
 queue.add(root);
 root.level = 0;
 while (!queue.isEmpty()) {
  BSTNode current = queue.poll();//look up what this function does in the Java Documentation
  nodes.add ( current );

  //Enqueue (add) left child if it isn't null  
  BSTNode a = current.leftChild;
  if ( a != null ) {
   queue.add (a);
   a.level = current.level + 1;
  }
 
  // xxx to be finished ...
  //Enqueue (add) right child if it isn't null  
 }
 return nodes ;
}

//counts the number of nodes in the tree
public int count() {
 // xxx to be finished ...
}

public int countEvenOdd(int remainder) {
 // xxx to be finished ...
 ArrayList  nodes = collectNodesByLevelOrder() ;
 int n = 0 ;
 for (BSTNode curr: nodes ) {
  if (curr.data%2 == remainder ) n++;
 }
 return n;
}
public int countOdds() {
 // xxx to be finished ...
 // hints: use countEvenOdd
}
 

public int countEvens() {
 // xxx to be finished ...
 // hints: use countEvenOdd
}


//returns the sum of the data in the tree
public int sum() {
 // xxx to be finished ...
}

//max length path from root to leaf node
public int height() {
 // xxx to be finished ...
}


//This method creates a test tree that you can use as
//you build out your find and insert methods
public static ArrayList genTrees (){
 // xxx Below are the testcases used for the questions in the lab report.
 int[] a = {11,7,2,8,15} ;
 int[] b = {  4,2,1,3, 6,5,7,10,11 };
 int[] c = {  14,2,1,3, 16,5,17,10,11 };
 int[] d = {11,7,2,8,15,10,3} ;
 int[][]arr = {a,b,c,d};

 ArrayList trees = new ArrayList ();
 
 for (int[] x: arr) {
  BinarySearchTree bst = new BinarySearchTree(9);
  for (int i: x ) {
   bst.insert ( i) ;
  }
  trees.add ( bst );
 }

 return trees;
}

public String toString() {
 ArrayList  nodes = collectNodesByLevelOrder() ;
 ArrayList  inorder = collectNodesByInOrder() ;
 int level = 0;
 int pos = -1;
 ArrayList arr = new ArrayList ();
 String blanks = " ".repeat(100);
       char[] ch = blanks.toCharArray();
 for (BSTNode curr: nodes ) {
  int h = curr.level ;
  if ( h != level ) {
   arr.add( new String(ch) );
         ch = blanks.toCharArray();
  }
  BSTNode a = curr.leftChild;
  BSTNode b = curr.rightChild;
  int m = 6;
           int p = inorder.indexOf (curr)*m;
  int j = p;
  int k = p;
  if ( a != null) {
   j = inorder.indexOf (a)*m+1;
   ch[j-1] = '+';
  }
  if ( b != null) {
   k = inorder.indexOf (b)*m;
   ch[k] = '+';
  }
           for (int i=j; i            String x = String.format ("%s", curr) ;
  if ( curr==root ) {
            x = String.format ("(%s)", curr) ;
  }
  for (int i=0; i    ch[p+i] = x.charAt(i) ;
  }  
           level =  h;
 }
 arr.add( new String(ch) );
 String s = "";
 for (String a: arr ) {
  s += a + "";
 }
 return s;
}

public static void testTree ( BinarySearchTree bst ) {
 //DO LOTS OF TESTING!!
       
 System.out.println(bst);
 System.out.println("height = " + bst.height() );
 System.out.println("sum of data in the tree = " + bst.sum() );
 System.out.println("number of even integers in the tree = " + bst.countEvens() );
 System.out.println("number of odd integers in the tree = " + bst.countOdds() );

 bst.inOrder();
 bst.preOrder();
 bst.postOrder();
 bst.levelOrder();
}
public static void main(String[] args) {
       ArrayList trees = genTrees();
 int i = 1 ;
 for (BinarySearchTree bst: trees) {
  String s = "----------------------------";
  System.out.println( s + "Tree " + i+ s +"");
  testTree (bst );
  i++;
  System.out.println();
 }
}
 

}

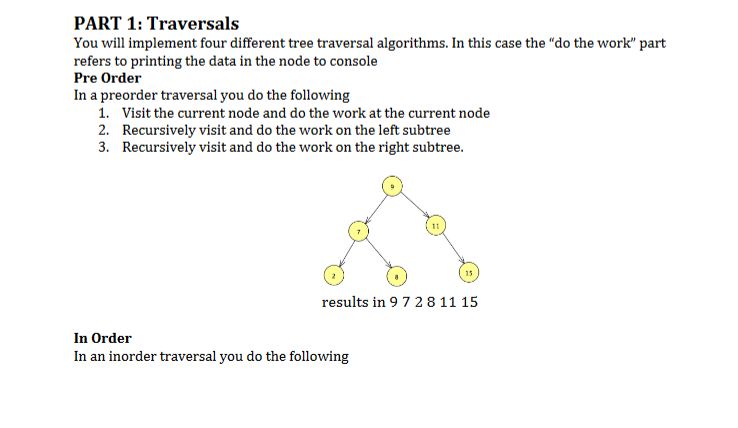
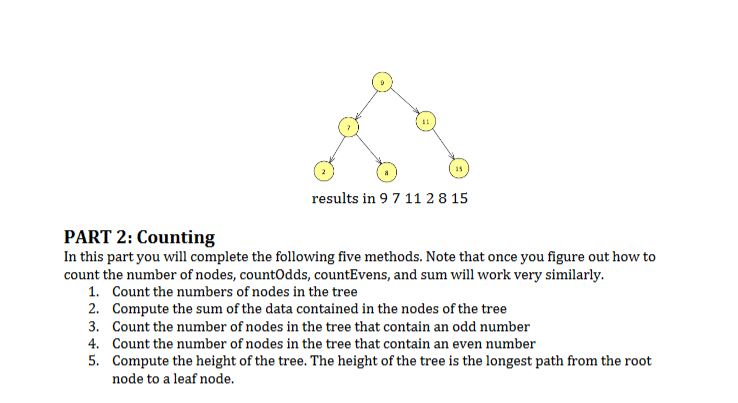
PART 1: Traversals You will implement four different tree traversal algorithms. In this case the "do the work" part refers to printing the data in the node to console Pre Order In a preorder traversal you do the following 1. Visit the current node and do the work at the current node 2. Recursively visit and do the work on the left subtree 3. Recursively visit and do the work on the right subtree. 15 results in 9 7 28 11 15 In Order In an inorder traversal you do the following