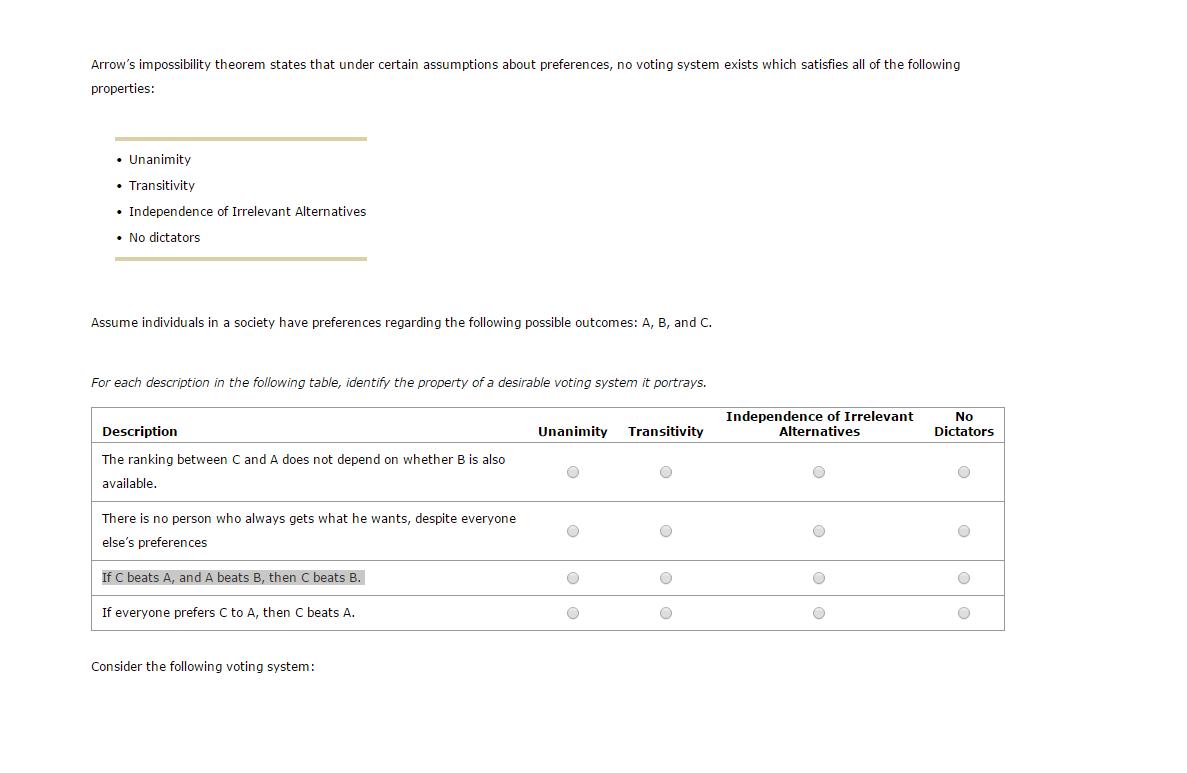
Arrow's impossibility theorem states that under certain assumptions about preferences, no voting system exists which satisfies all of the following properties: . Unanimity Transitivity Independence of Irrelevant Alternatives . No dictators Assume individuals in a society have preferences regarding the following possible outcomes: A, B, and C. For each description in the following table, identify the property of a desirable voting system it portrays. Description The ranking between C and A does not depend on whether B is also available. There is no person who always gets what he wants, despite everyone else's preferences If C beats A, and A beats B, then C beats B. If everyone prefers C to A, then C beats A. Consider the following voting system: Unanimity Transitivity O O O Independence of Irrelevant Alternatives O O No Dictators O O O In a pairwise voting system, voters first choose between two outcomes, then the winner of that vote gets paired against the remaining outcome to determine the voters' choice. Suppose someone suggests choosing first between A and B and then comparing the winner to C. This results in the voters choosing C. However, if the voters choose first between B and C and then compare the winner to A, the voters end up with B instead. Which property does this voting method violate according to Arrow's impossibility theorem? Transitivity Unanimity Independence of irrelevant alternatives No dictators