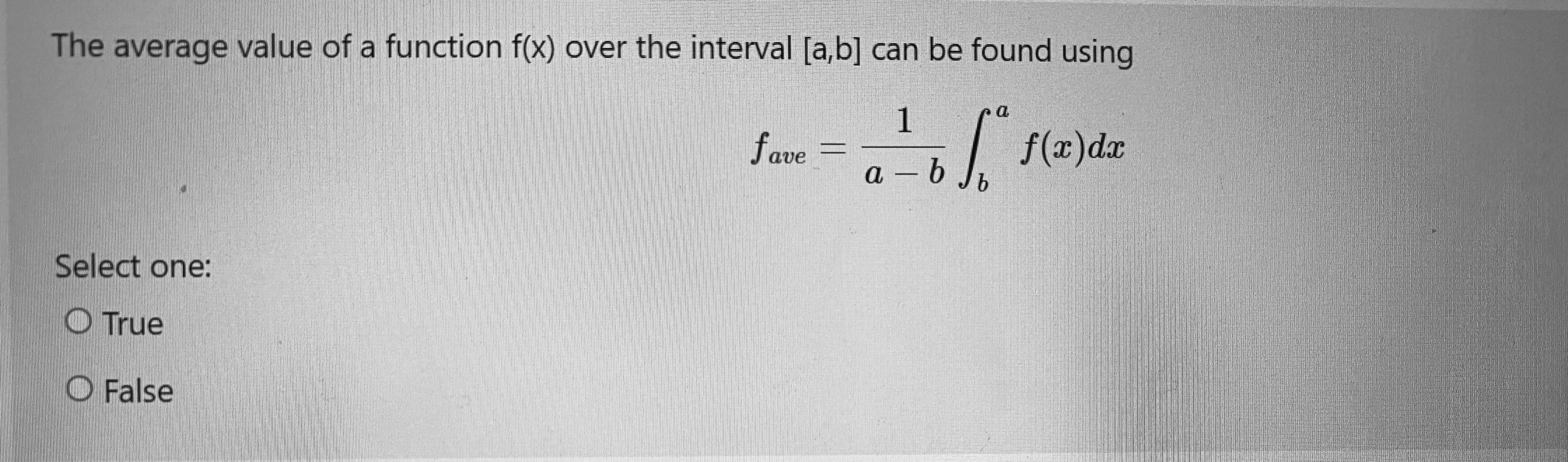
As a car accelerates, it does not accelerate at a constant rate; rather, the acceleration is variable. The quadratic function a(t) = -0.70t2 + 1.44t + 10.44 describes the acceleration in seconds. Compute the average value of a(t) to estimate the average acceleration between t = 0 and t = 8.7 seconds. Round your answer to five decimal places. Answer:When approximationg the area under the curve of f(x) using a right-endpoint Riemann sum, the height of the nth rectangle is determined using b and the function f(x). Select one: True FalseTime left 0: onsider the parabola p(x) - -7.7x2 + 3.9x + 7.4. For which interval [A, B] is p(x ) dx A as large as possible? A note about the choices: for some incomprehensible reason eClass sometimes switches the position of A and B. Read each option very carefully, as your interval might be a backwards version of what eClass is showing as an option. O a. [4.9125, 2.8875] O b. [1.0125, -1.0125] c. [0.75926, -1.26575] O d. [-7.7. 3.9] O e. [0.2532 , -0.2532]The average value of a function f(x) over the interval [a,b] can be found using a fave = f(x) dx a - b Jb Select one: True False