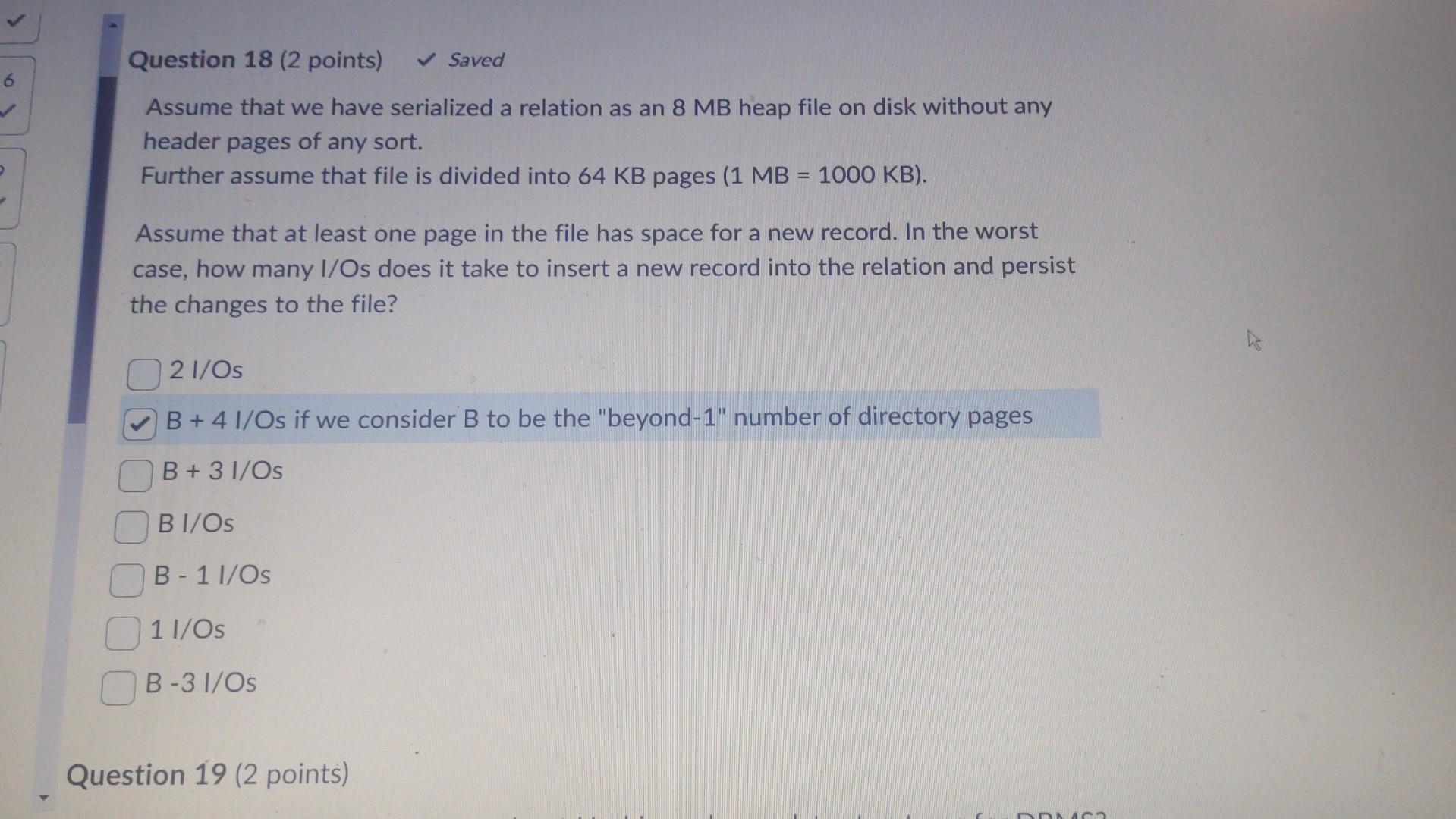
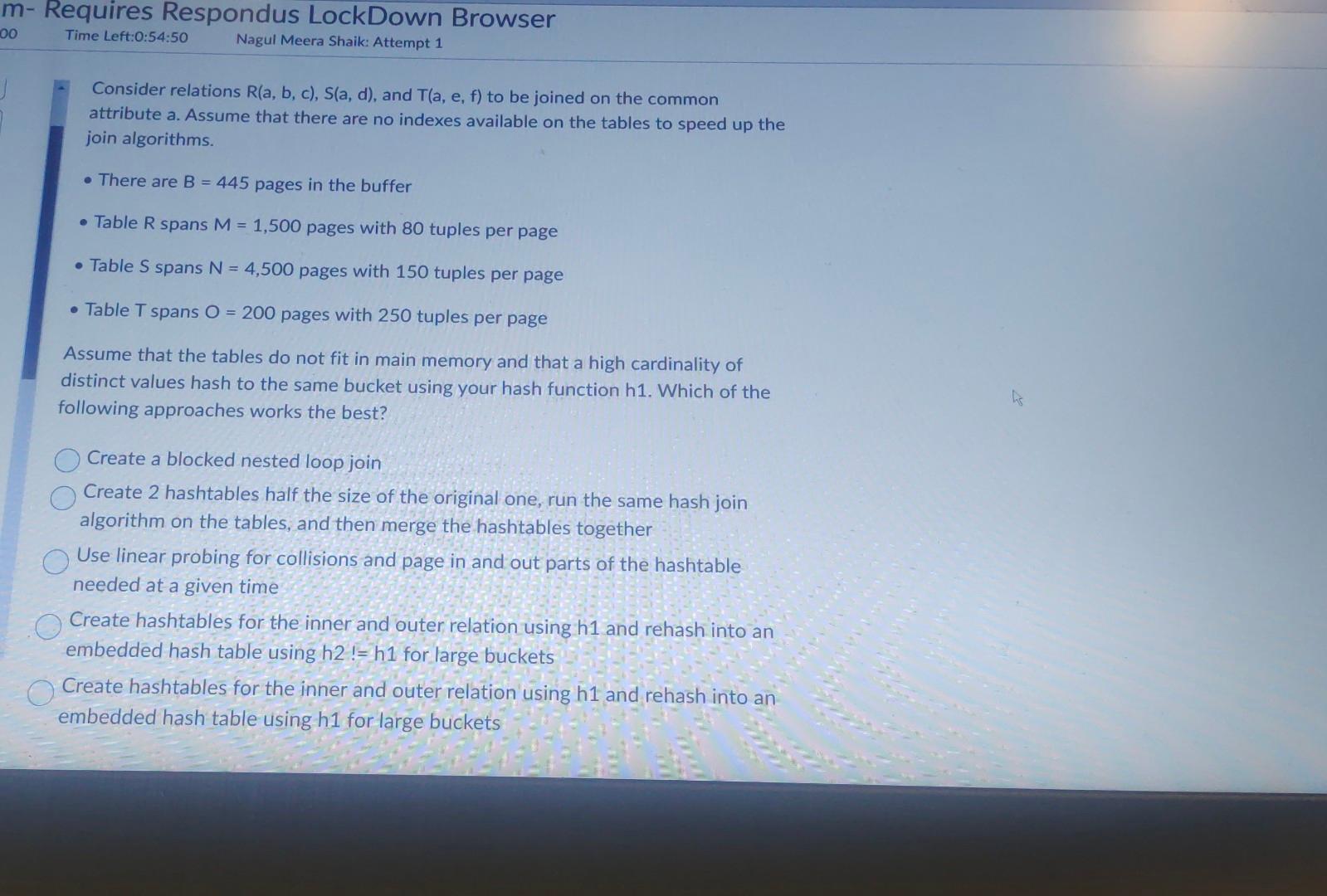
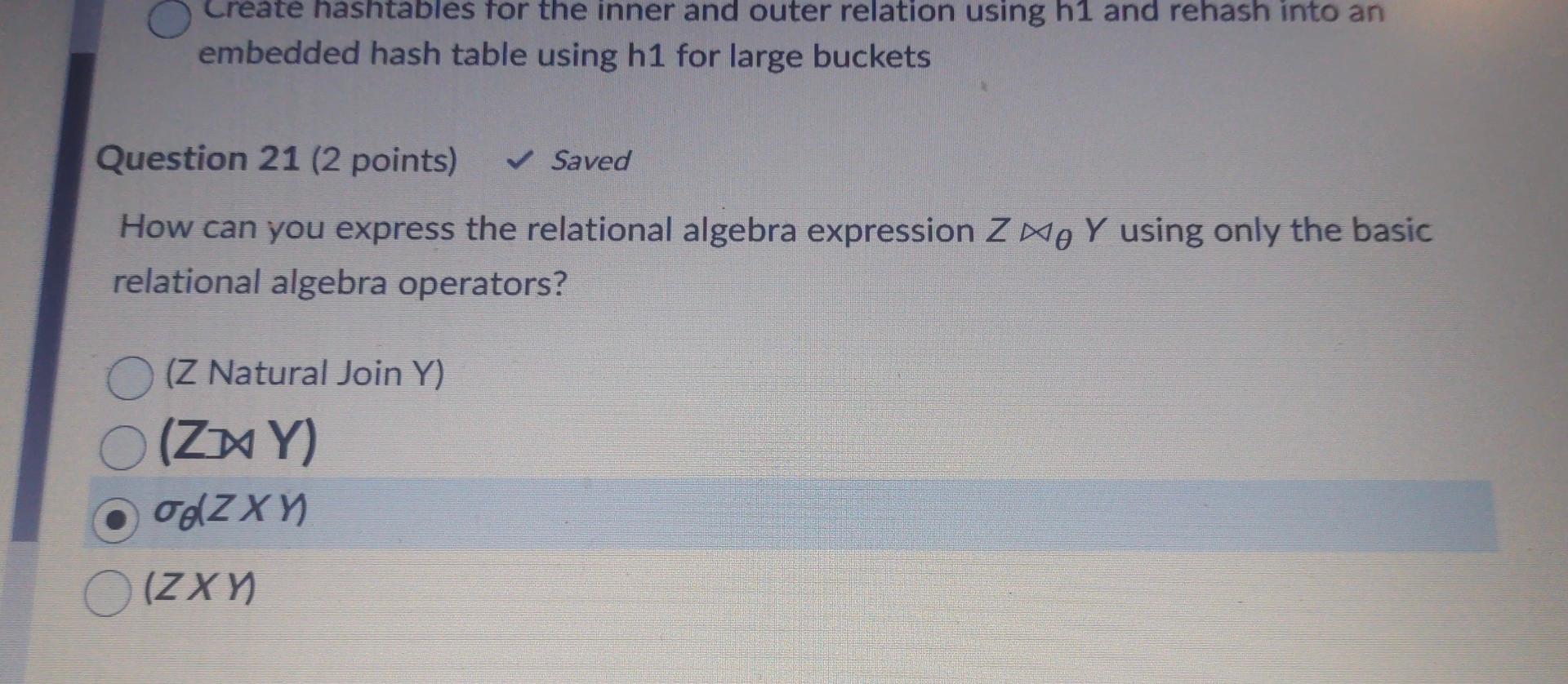
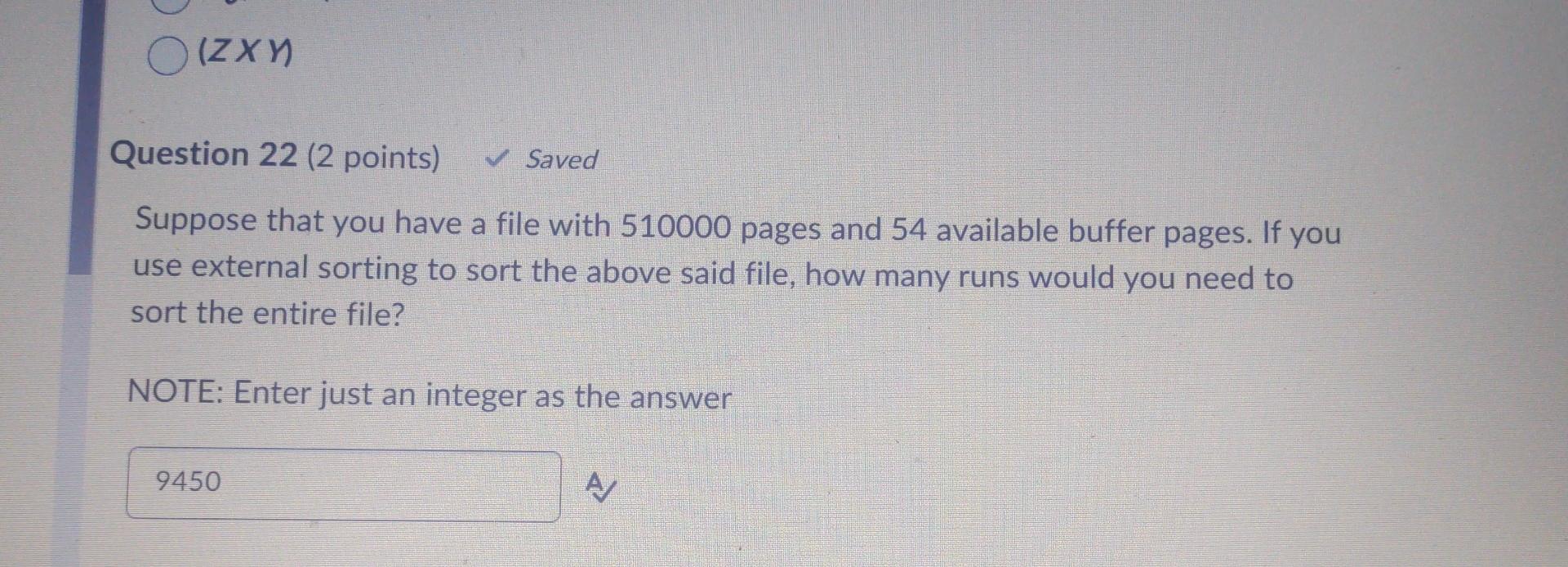
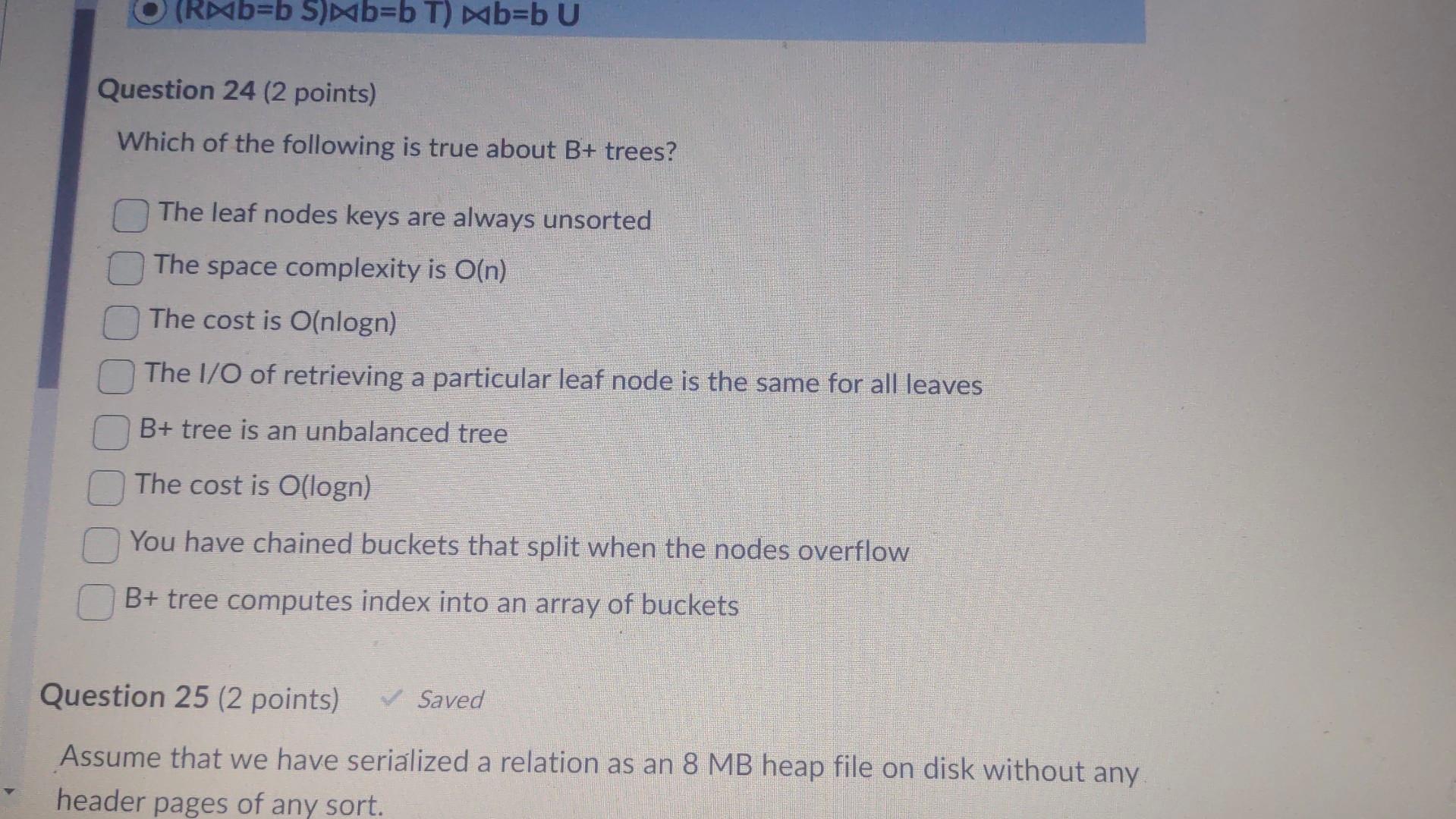
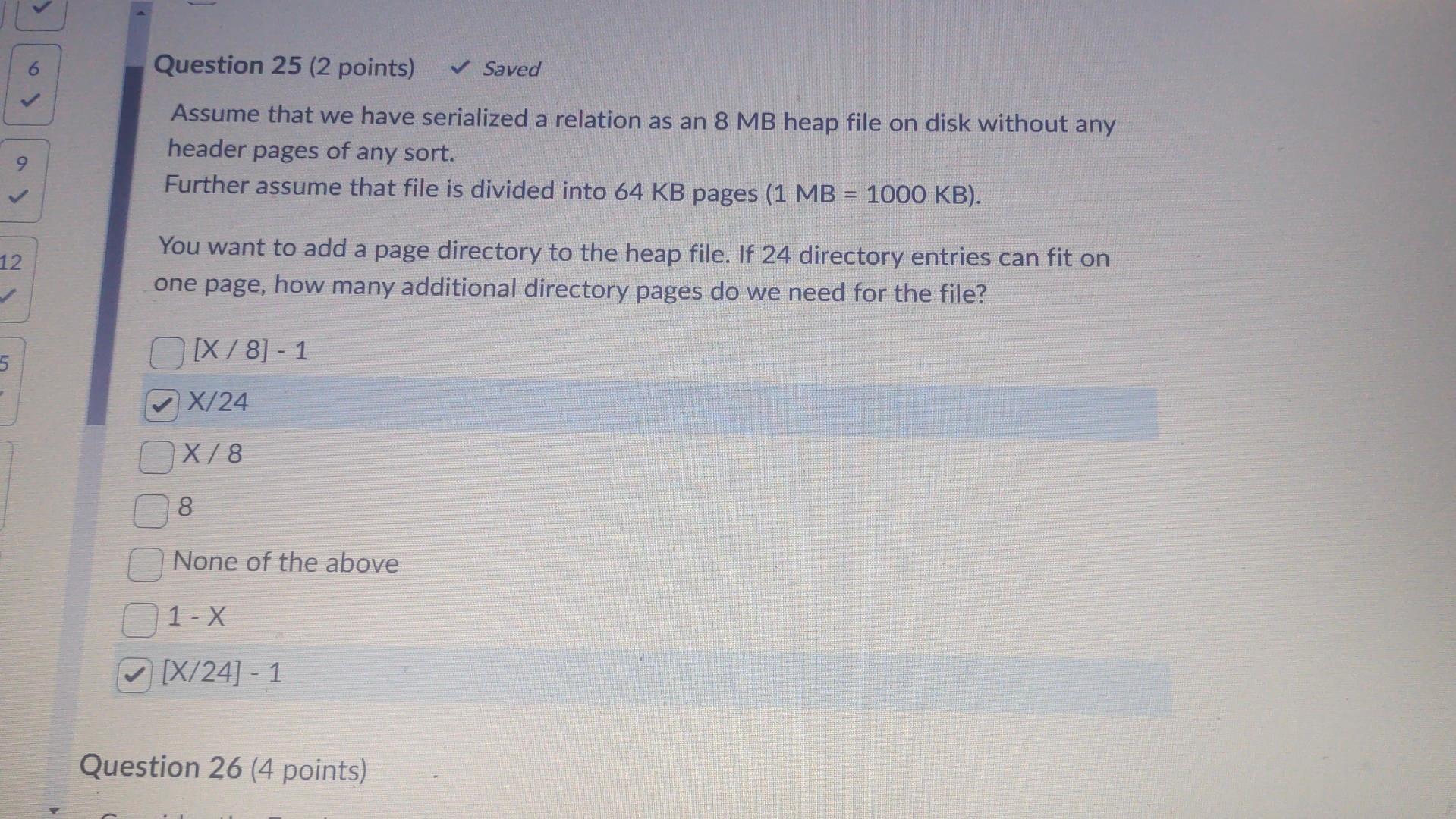
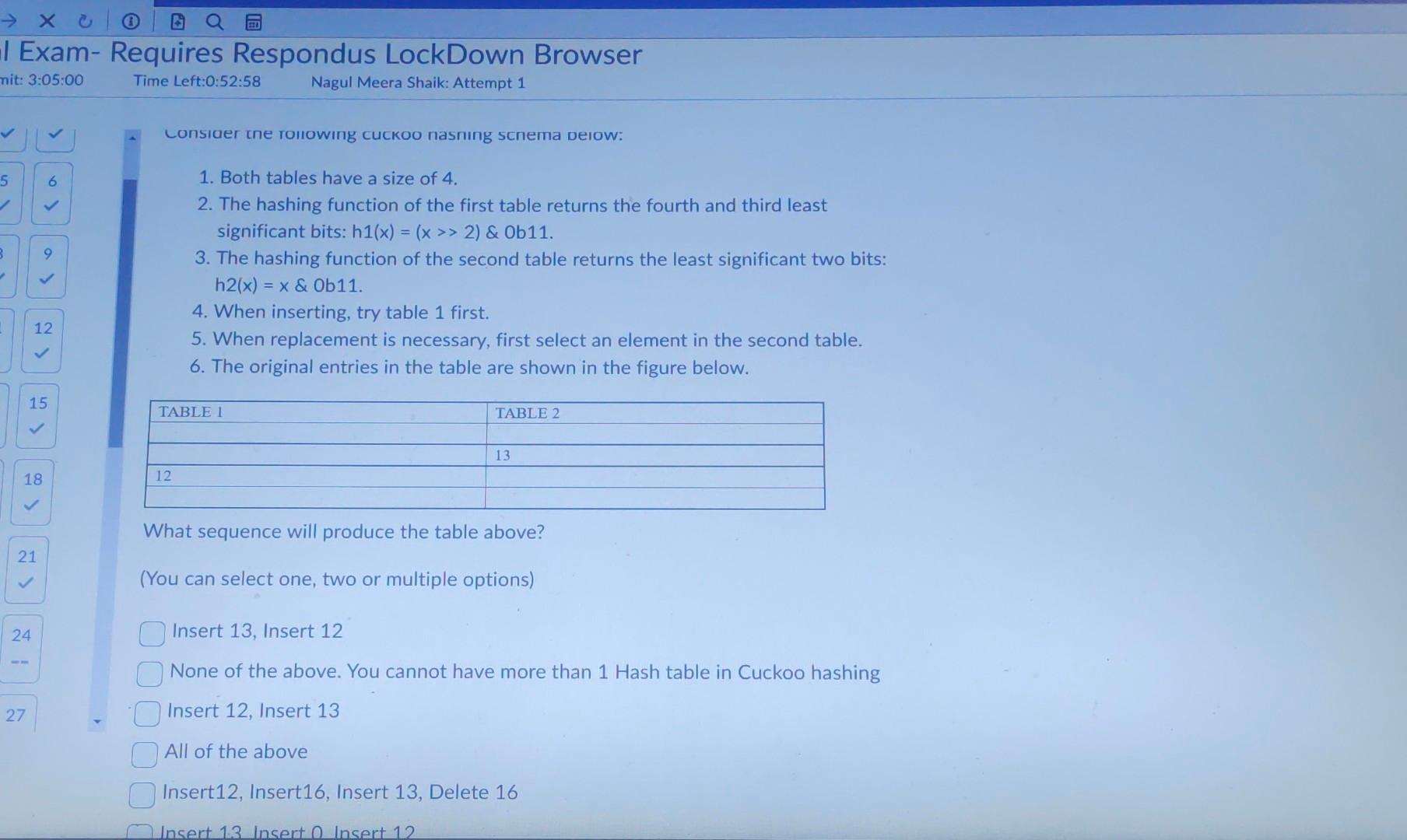
Assume that we have serialized a relation as an 8MB heap file on disk without any header pages of any sort. Further assume that file is divided into 64KB pages ( MB=1000KB ). Assume that at least one page in the file has space for a new record. In the worst case, how many I/Os does it take to insert a new record into the relation and persist the changes to the file? 2l/Os B+4 I/Os if we consider B to be the "beyond-1" number of directory pages B+3I/Os BI/Os B1I/Os 1l/Os B3I/Os Which of the following is correct about Hashing scheme data structures for DBMS? (You can choose one, two or more than 2 answers) Time complexity for Cuckoo hashing is O(n2) Robinhood Hashing is a dynamic hashing Chained hashing always splits a bucket that overflows Redundant keys can help handle non-unique key index Extendible hashing lets buckets grow infinitely - Consider relations R(a,b,c),S(a,d), and T(a,e,f) to be joined on the common attribute a. Assume that there are no indexes available on the tables to speed up the join algorithms. - There are B=445 pages in the buffer - Table R spans M=1,500 pages with 80 tuples per page - Table S spans N=4,500 pages with 150 tuples per page - Table T spans O=200 pages with 250 tuples per page Assume that the tables do not fit in main memory and that a high cardinality of distinct values hash to the same bucket using your hash function h1. Which of the following approaches works the best? Create a blocked nested loop join Create 2 hashtables half the size of the original one, run the same hash join algorithm on the tables, and then merge the hashtables together Use linear probing for collisions and page in and out parts of the hashtable needed at a given time Create hashtables for the inner and outer relation using h1 and rehash into an embedded hash table using h2!= h1 for large buckets Create hashtables for the inner and outer relation using h1 and rehash into an embedded hash table using h1 for large buckets Create nashtables tor the inner and outer relation using h1 and rehash into an embedded hash table using h1 for large buckets Question 21 (2 points) Saved How can you express the relational algebra expression ZY using only the basic relational algebra operators? (Z Natural Join Y) (ZY) (ZY) (ZY) Suppose that you have a file with 510000 pages and 54 available buffer pages. If you use external sorting to sort the above said file, how many runs would you need to sort the entire file? NOTE: Enter just an integer as the answer Which of the following is true about B+ trees? The leaf nodes keys are always unsorted The space complexity is O(n) The cost is O(nlogn) The 1/0 of retrieving a particular leaf node is the same for all leaves B+ tree is an unbalanced tree The cost is (logn) You have chained buckets that split when the nodes overflow B+ tree computes index into an array of buckets Question 25 (2 points) Saved Assume that we have serialized a relation as an 8 MB heap file on disk without any header pages of any sort. Assume that we have serialized a relation as an 8MB heap file on disk without any header pages of any sort. Further assume that file is divided into 64KB pages (1MB=1000KB). You want to add a page directory to the heap file. If 24 directory entries can fit on one page, how many additional directory pages do we need for the file? [X/8]1X/24X/88 None of the above 1-X [X/24]1 Question 26 (4 points) Lonsider tne rolowing cuckoo nasnng scnema Delow: 1. Both tables have a size of 4 . 2. The hashing function of the first table returns the fourth and third least significant bits: h1(x)=(x>>2)&0b11. 3. The hashing function of the second table returns the least significant two bits: h2(x)=x& Ob11. 4. When inserting, try table 1 first. 5. When replacement is necessary, first select an element in the second table. 6. The original entries in the table are shown in the figure below. What sequence will produce the table above? (You can select one, two or multiple options) Insert 13, Insert 12 None of the above. You cannot have more than 1 Hash table in Cuckoo hashing Insert 12, Insert 13 All of the above Insert12, Insert16, Insert 13 , Delete 16