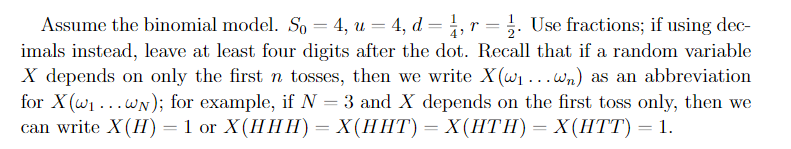
Assume the binomial model. So = 4, u = 4, d = , r = 3. Use fractions; if using dec- imals instead, leave at least four digits after the dot. Recall that if a random variable X depends on only the first n tosses, then we write X(wi...wn) as an abbreviation for Xw1 ...wn); for example, if N = 3 and X depends on the first toss only, then we can write X (H) = 1 or X(HHH) = X(HHT) = X(HTH) = X(HTT) = 1. (2) (12+12+8=32 points) Suppose N = 2. S, (1+r)" that S E1[S2] 1+r (b) You have a (European) security which pays you $5 if the stock price has jumped twice. Use the backward algorithm to find Xn and An for n (c) You have a (European) security which pays you $5 if the stock price has jumped twice. Use the conditional expectation to find Xn for n 0,1. -0,1. Assume the binomial model. So = 4, u = 4, d = , r = 3. Use fractions; if using dec- imals instead, leave at least four digits after the dot. Recall that if a random variable X depends on only the first n tosses, then we write X(wi...wn) as an abbreviation for Xw1 ...wn); for example, if N = 3 and X depends on the first toss only, then we can write X (H) = 1 or X(HHH) = X(HHT) = X(HTH) = X(HTT) = 1. (2) (12+12+8=32 points) Suppose N = 2. S, (1+r)" that S E1[S2] 1+r (b) You have a (European) security which pays you $5 if the stock price has jumped twice. Use the backward algorithm to find Xn and An for n (c) You have a (European) security which pays you $5 if the stock price has jumped twice. Use the conditional expectation to find Xn for n 0,1. -0,1