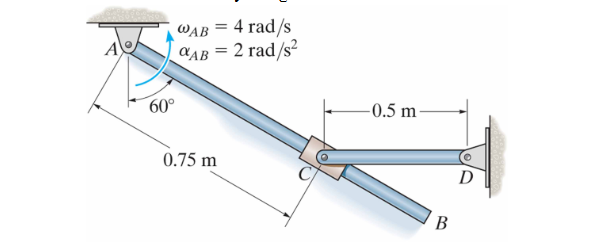
At the instant shown, rod AB has an angular velocity of $4$rad$/$s and an angular acceleration of $2$ rad$/$s$.$ Determine the angular velocity and acceleration of rod CD at this instant. The collar at C is pin connected to CD and slides freely along AB$.$ Please solve with MATLAB code template provided$>$ the acceleration is correct but I cant figure out what to change in order to make the velocity to be $-56\mathrm{.}25,$ which should be the correct answer unless I am mistaken. $\%$ Clear memory and screen

clear all;

clc;

$\%$ Define unknown quantities in x$-$y system

$\%$ abc $=$ Acceleration of B wrt C on beam CD in i direction

$\%$ vbc $=$ Velocity of B wrt C on beam CD in i direction

$\%$ xacd $=$ Angular acceleration of beam CD in $-$k direction

$\%$ xvcd $=$ Angular velocity of beam CD in $-$k direction

syms abc vbc xacd xvcd;

$\%$ Create Unit Vectors in x$-$y coordinates

i $=[1,0,0]$;

j $=[0,1,0]$;

k $=[0,0,1]$;

$\%$ Create Unit Vectors in X$-$Y coordinates $($R is rotation Matrix$)$

Theta $=30$; $\%$ Angle from X$-$axis to x$-$axis

R $=[[$cosd$($Theta$),-$sind$($Theta$),0]$; $...$

$[$sind$($Theta$),$ cosd$($Theta$),0]$; $[0,0,1]]$;

XYZ $=$ R$*[$i;j;k$]$;

I $=$ XYZ$(1,$:$)$;

J $=$ XYZ$(2,$:$)$;

K $=$ XYZ$(3,$:$)$;

$\%$ Set known quantities for Beam AB $($no slider connection$).$

xVab $=4*$k; $\%$ Angular Velocity of Beam AB

xAab $=-2*$k; $\%$ Angular Acceleration of Beam AB

Rba $=\mathrm{.}75*$i$+$; $\%$ Vector from A to B in X$-$Y coordinates

$\%$ Calculate velocity and acceleration of point B

$\%$ due to rotation of Beam AB $($no slider connection$).$

Vb$1=$ cross$($xVab$,$Rba$)$;

Ab$1=$ cross$($xAab$,$Rba$)-$ dot$($xVab$,$xVab$)*$Rba;

$\%$ Set Motion of moving reference frame $($x$-$y wrt X$-$Y$).$

xV $=-$xvcd$*$k;

xA $=-$xacd$*$k;

$\%$ Set Motion of B wrt moving frame $($x$-$y$).$

Rbc $=-\mathrm{.}433*$i$-\mathrm{.}25*$j;

Vbc $=-$vbc$*$i;

Abc $=$ abc$*$i;

$\%$ Calculate velocity and acceleration of point B

$\%$ due to rotation of beam CD $($slider connection$).$

Vb$2=$ cross$($xV$,$Rbc$)+$ Vbc;

Ab$2=$ cross$($xA$,$Rbc$)+$ cross$($xV$,$cross$($xV$,$Rbc$))+2*$cross$($xV$,$Vbc$)+$ Abc;

$\%$ Set velocity and acceleration equations equal for point B and solve.

Z $=[$Vb$1(1)-$Vb$2(1),$Vb$1(2)-$Vb$2(2),$Ab$1(1)-$Ab$2(1),$Ab$1(2)-$Ab$2(2)]$;

$[$abc$,$vbc$,$xacd,xvcd$]=$ solve$($Z$(1),$Z$(2),$Z$(3),$Z$(4))$;

abc $=$ eval$($abc$)$

vbc $=$ eval$($vbc$)$

xacd $=$ eval$($xacd$)$

xvcd $=$ eval$($xvcd$)$