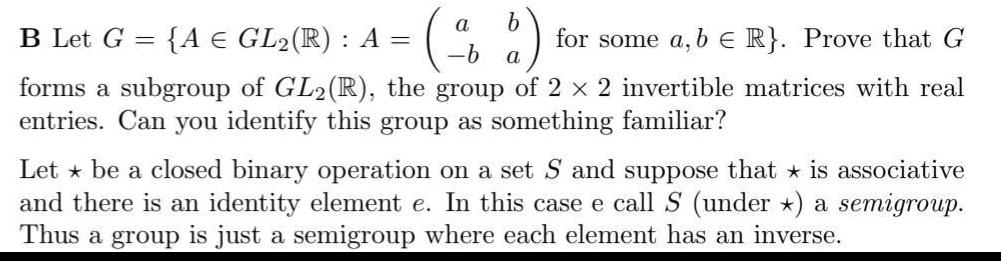
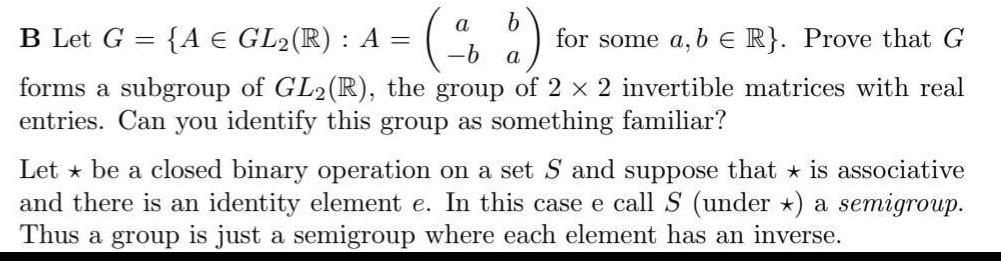
b B Let G A E GL R A d for some a b E R Prove that G a forms a subgroup of GL2 R the group of 2 x 2 invertible matrices with real entries Can you identify this group as something familiar Let be a closed binary operation on a set S and suppose that is associative and there is an identity element e In this case e call S under a semigroup Thus a group is just a semigroup where each element has an inverse