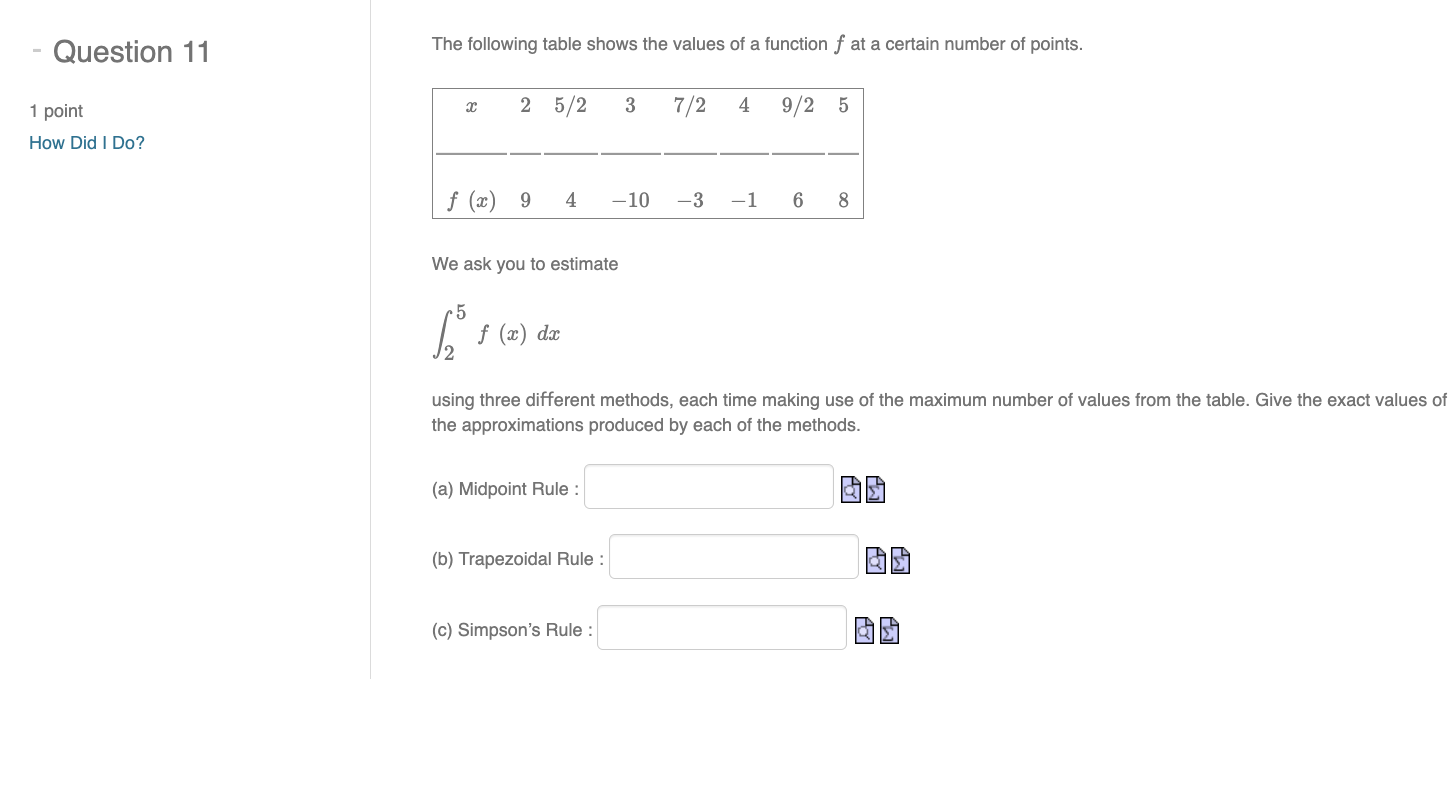
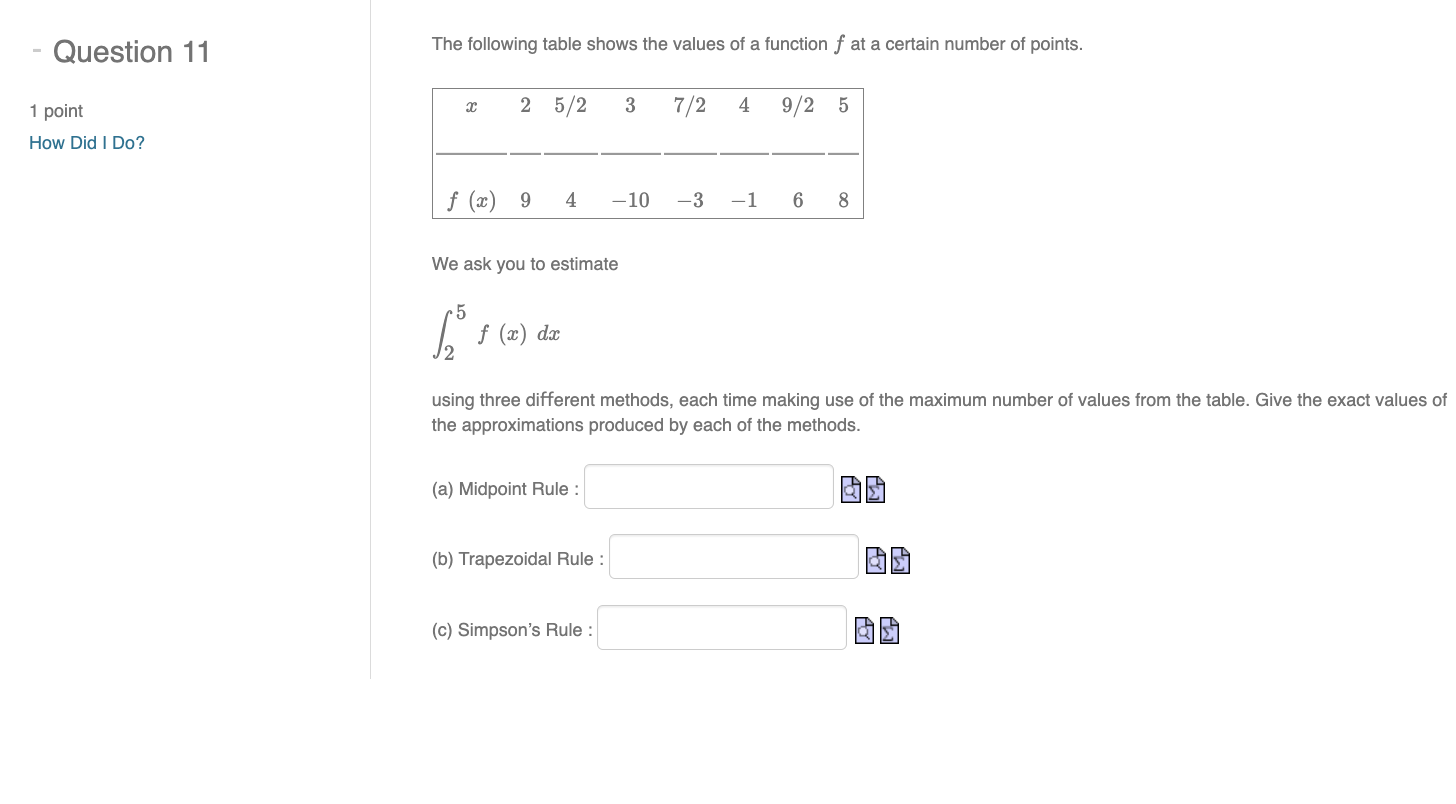
' b QUEStIDn 1 2 The midpoint rule does notoompute an integral / f(9:) do exactly. The error is the diflerence between the midpoint rule a 1 point estimate Mn and the actual value; we cannot find the actual error unless we can evaluate the integral exactly. We have a How Did I Do? formula for an error bound on the midpoint rule, depending on f, a, b and n: we can calculate the error bound without evaluating the integral exactly. The important theorem is that the error on the estimate will always be less than or equal to the error bound, in absolute value. Consider f(:} : (an 4)5 on the interval [0,6]. Compute f"[a:) : 20(x-4)"3 [a What is the maximum value of |f"($}| on the interval [0, 6] ? la a The error bound on Mn. as a function of n, is therefore 3(a) : a 6 Therefore, to be sure that Mn, is within 10'2 of the true value of the integral / (m 4}5 (1.1:. we need B(n) S 1072, 0 which means we must choose 1! = la a (Round up to the nearest integer.) - Question 11 The following table shows the values of a function f at a certain number of points. 1 point 2 5/2 3 7/2 4 9/2 5 How Did I Do? f (a) 9 4 -10 -3 -1 6 8 We ask you to estimate ( f ( 2 ) da using three different methods, each time making use of the maximum number of values from the table. Give the exact values of the approximations produced by each of the methods. (a) Midpoint Rule : (b) Trapezoidal Rule : (c) Simpson's Rule