b.)

Using java, explore the bifurcation behavior of the logistic map

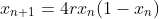
by plotting the fixed points as a function of r for r = 0.75 to r = 1.0. Divide the range [0.75,1.0] into 500 to 1000 (depending on your computer resources) discrete values of 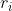. For each > 0.891, iterate from 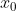= 0.7 for 600 times but only plot the last 300 values (all at the same 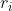). For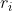

Here is the original code:

import org.opensourcephysics.controls.*; import org.opensourcephysics.display.*; import org.opensourcephysics.frames.PlotFrame; public class ChaoticMapApp extends AbstractSimulation { PlotFrame frame = new PlotFrame("x", "y", "Chaotic Map"); double t = 0, dt = 0.1; double x,y,xplot,yplot,term; int nspeed; final static double rcos = Math.cos(3.141592653*76.11/180.0); final static double rsin = Math.sin(3.141592653*76.11/180.0); Circle circle = new Circle(0, 0, 5); public void reset() { t = 0.0; frame.setPreferredMinMax(-1.0, 1.0, -1.0, 1.0); frame.setSize(600, 600); frame.setConnected(false); // frame.setMarkerSize(0,1); // frame.setMarkerSize(1,1); frame.setMarkerSize(2,0); // frame.setMarkerShape(0, Dataset.NO_MARKER); frame.addDrawable(circle); // frame.append(0, 0, 0); control.setValue("x0", "0.0"); control.setValue("y0", "0.441"); control.setValue("nspeed", "1"); initialize(); } /** * Initializes the simulation. */ public void initialize() { x = control.getDouble("x0"); y = control.getDouble("y0"); nspeed = control.getInt("nspeed"); t = 0.0; // frame.append(0, 0, 0); circle.setXY(0, 0); frame.setMessage("t="+decimalFormat.format(t), 1); } /** * Does a simulation step. */ protected void doStep() { for(int n = 0;n  rn + 1 = 4r.r.n (1--Fn)  rn + 1 = 4r.r.n (1--Fn)