Background :

Questions : How do I knew M(52)?

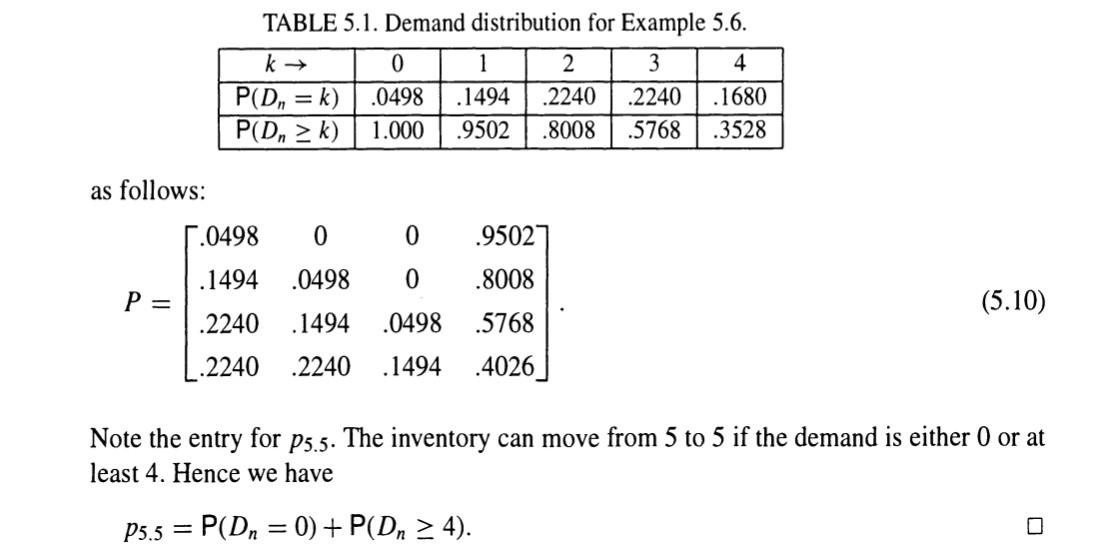
5.16. Consider the inventory system of Example 5.6. Compute the occupancy matrix M(52). Using this compute the expected number of weeks that Computers-R-Us starts with a full inventory (i.e., five PCs) during a year, given that it started the first week of the year with an inventory of five PCs. Example 5.6 (Inventory System). Computers-R-Us stocks a wide variety of PCs for retail sales. It is open for business Monday through Friday 8:00 a.m. to 5:00 p.m. It uses the following operating policy to control the inventory of Pentium PCs: At 5:00 p.m. Friday, the store clerk checks to see how many Pentium PCs are still in stock. If the number is less than 2 , then he orders enough PCs to bring the total in stock up to 5 at the beginning of the business day Monday. If the number in stock is 2 or more no action is taken. The demand for the Pentium PCs during the week is a Poisson random variable with mean 3. Any demand that cannot be immediately satisfied is lost. Develop a stochastic model of the inventory of the Pentium PCs at Computers-R-Us. Let Xn be the number of Pentium PCs in stock in Computers-R-Us at 8:00 a.m. Monday of the nth week. Let Dn be the number of Pentium PCs demanded during the nth week. Then the number of PCs left in the store at the end of the week is max(XnDn,0). If XnDn2, then there are 2 or more Pentium PCs left in the store at 5:00 p.m. Friday of the nth week. Hence no more PCs will be ordered that weekend, and we will have Xn+1=XnDn. On the other hand, if XnDn1, there is 1 or 0 Pentiums left in the store at the end of the week. Hence enough will be ordered over the weekend so that Xn+1=5. Putting these observations together we get Xn+1={XnDn5ifXnDn2ifXnDn1 It then follows that the state space of {Xn,n0} is {2,3,4,5}. Now assume that the demands from week to week are independent of each other and of the inventory in the store. Then we can show that {Xn,n0} is a DTMC. We have, for j=2,3,4 and i=j,j+1,,5 P(Xn+1=jXn=i,Xn1,,X0)=P(XnDn=jXn=i,Xn1,,X0)=P(iDn=jXn=i,Xn1,,X0)=P(Dn=ij) Similarly, P(Xn+1=5Xn=i)=P(XnDn1Xn=i)=P(Dni1) for i=2,3,4. Using the fact that Dn is a P(3) random variable, we get Table 5.1. Using the data in this table we can compute the transition probability matrix of the DTMC {Xn,n0} TABLE 5.1. Demand distribution for Example 5.6. as follows: P=.0498.1494.2240.22400.0498.1494.224000.0498.1494.9502.8008.5768.4026 Note the entry for p5.5. The inventory can move from 5 to 5 if the demand is either 0 or at least 4. Hence we have p5.5=P(Dn=0)+P(Dn4)