Question: Based off this algorithm: Please answer the following: tvorio oo CoinChange(d, N) 1. n = length[d] 2. for i = 1 ton 3. C[i,j] =
Based off this algorithm:
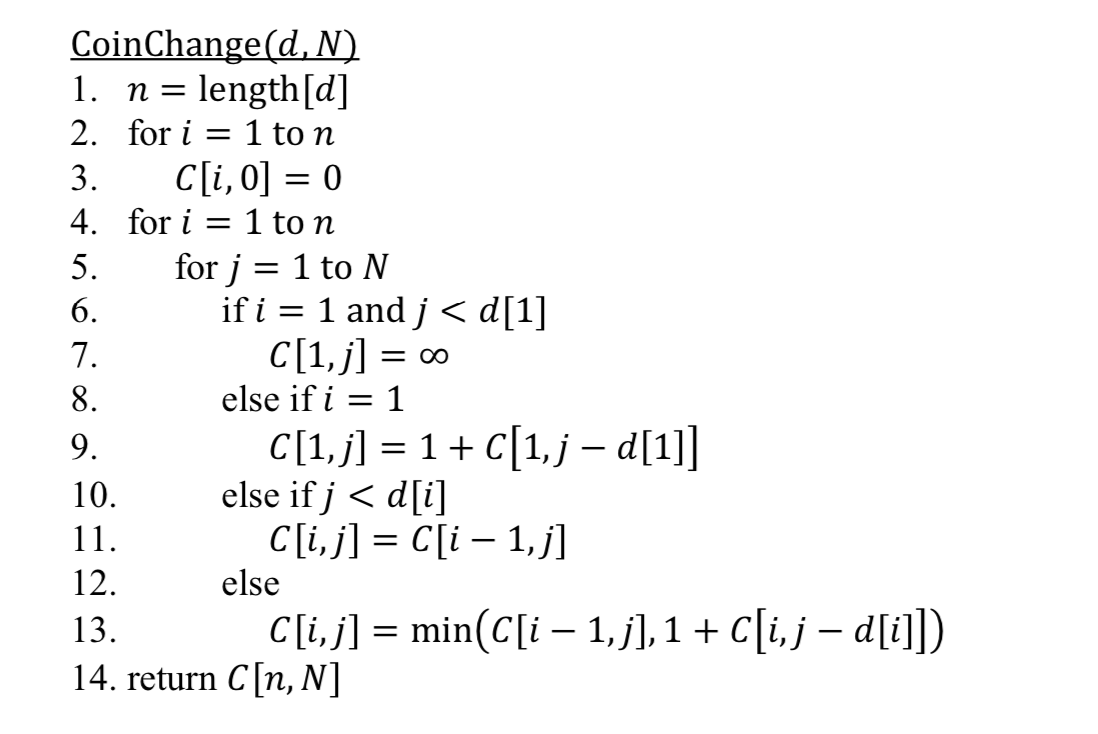 Please answer the following:
Please answer the following:
![1. n = length[d] 2. for i = 1 ton 3. C[i,j]](https://s3.amazonaws.com/si.experts.images/answers/2024/09/66dfd8007013d_85566dfd7ffc8c5b.jpg)
tvorio oo CoinChange(d, N) 1. n = length[d] 2. for i = 1 ton 3. C[i,j] = 0 4. for i = 1 ton for j = 1 to N if i = 1 and j 1, and 1 sisn, i.e. d = (1, b, b2, ...,bn-1). Does the greedy strategy always produce an optimal solution in this case? Either prove that it does, or give a counter-example. c. Let d = 1 and 2di s di+1 for 1 si sn - 1. Does the greedy strategy always produce an optimal solution in this case? Either prove that it does, or give a counter- example. tvorio oo CoinChange(d, N) 1. n = length[d] 2. for i = 1 ton 3. C[i,j] = 0 4. for i = 1 ton for j = 1 to N if i = 1 and j 1, and 1 sisn, i.e. d = (1, b, b2, ...,bn-1). Does the greedy strategy always produce an optimal solution in this case? Either prove that it does, or give a counter-example. c. Let d = 1 and 2di s di+1 for 1 si sn - 1. Does the greedy strategy always produce an optimal solution in this case? Either prove that it does, or give a counter- example
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


