Based on problem 3-28:

1. Why is the left hand side of the max plot A acre constraint equation (highlighted) equal to O5 or maximize profit (=sumproduct(B5:J5, B4:J4)) + L2 (no idea what that is), shouldn't it be equal to the sumproduct like everything else?

2. Why is there only proportion of plot A to B and B to C constraints, but no C to A, I thought they all have to be the same?

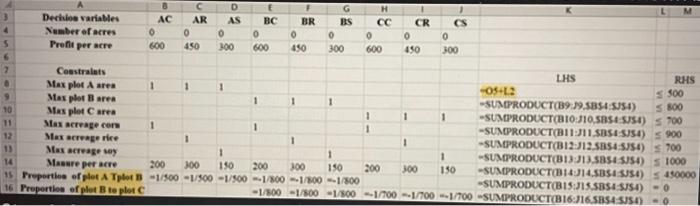
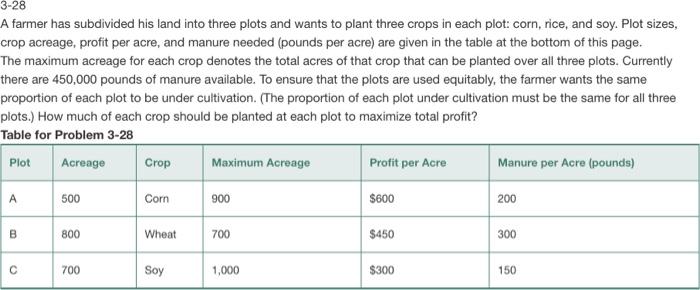
\begin{tabular}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|} \hline & A & B & c & D & E & 7 & G & H & 1 & 1 & K & L & M \\ \hline 3 & Deribise variables & AC & AR & As & BC & BR & BS & cC & CR & cs & & & \\ \hline 4 & Number of acres & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & & & \\ \hline 5 & Prefli per acre & 600 & 450 & 300 & 600 & 450 & 300 & 600 & 450 & 300 & & & \\ \hline 6 & & & & & & & & & & & & & \\ \hline & Cesstraints & & & & & & & & & & LHS & & RHS \\ \hline - & Max plot A arez & 1 & 1 & 1 & & & & & & & 05+12 & & 500 \\ \hline 9 & Max plot B aren & & & & 1 & 1 & 1 & & & & -5UMTRODUCT(B9.59.5BS4:SUS4) & & 800 \\ \hline 10 & Mes plet Caren & & & & & & & 1 & 1 & 1 & & & 700 \\ \hline 11 & Max acreage cen & 1 & & & 1 & & & 1 & & & & & 900 \\ \hline 12 & Mex actomger rice & & 1 & & & I & & & 1 & & -sUMERODUCT(B12:J12.sasu-suse) & & 700 \\ \hline 1) & Mas acreage sey & & & 1 & & & 1 & & & 1 & -sUMPRODUCT(B13:Ji3.sasususa) & & 1000 \\ \hline 14 & Masure per acre & 200 & 300 & 190 & 200 & 300 & 150 & 200 & 300 & 150 & -sUMPROOUCT(BIAJIA.SBS4:SUSU) & & 450000 \\ \hline is & Freportioe of plet A Tplot B & 1/400 & 1/500 & 1/300 & 1/800 & 1/200 & 1/800 & & & & & - & \\ \hline 16 & Preportion of plet B te plet C & & & & 1/800 & 1/800 & 1/500 & 1/700 & 1/700 & 1/700 & -sUMPRODUCT(B16:16.5Bs4-SUSO) & = & \\ \hline \end{tabular} A farmer has subdivided his land into three plots and wants to plant three crops in each plot: corn, rice, and soy. Plot sizes, crop acreage, profit per acre, and manure needed (pounds per acre) are given in the table at the bottom of this page. The maximum acreage for each crop denotes the total acres of that crop that can be planted over all three plots. Currently there are 450,000 pounds of manure available. To ensure that the plots are used equitably, the farmer wants the same proportion of each plot to be under cultivation. (The proportion of each plot under cultivation must be the same for all three plots.) How much of each crop should be planted at each plot to maximize total profit