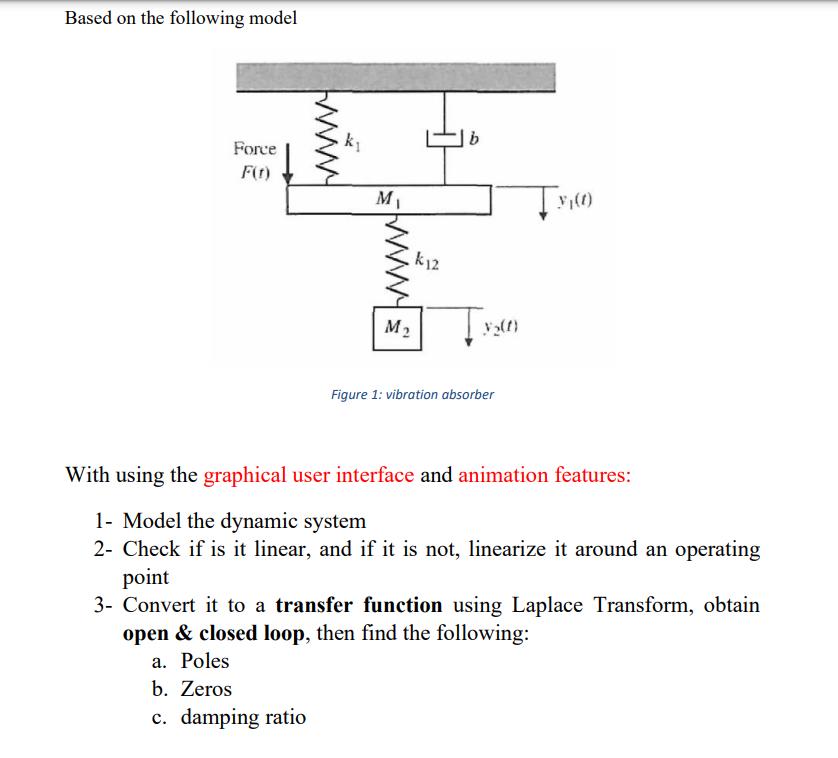
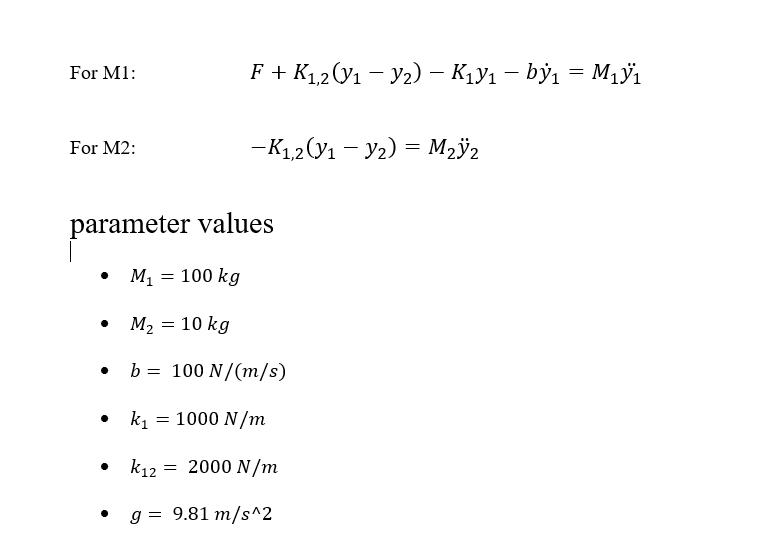
Based on the following model Force F(t) k M M k12 b V(1) Figure 1: vibration absorber Tx(0) With using the graphical user interface and animation features: 1- Model the dynamic system 2- Check if is it linear, and if it is not, linearize it around an operating point 3- Convert it to a transfer function using Laplace Transform, obtain open & closed loop, then find the following: a. Poles b. Zeros c. damping ratio d. natural frequency e. Is it overdamped, underdamped, or critical damping f. Zero-pole map g. Step response and find all the properties of the time domain (settling time, etc.) h. Impulse response and find all the properties of the time domain (settling time, etc.) 4- Obtain the state-space representation by finding Matrices A, B, C, D and state variables (plot the state variables versus time) 5- Check the stability For M1: For M2: parameter values M = 100 kg M = 10 kg b= 100 N/(m/s) k = 1000 N/m F + K1,2 (V - Y) - KV -by = M3 -K1,2(y1 - y2) = M2 k12 2000 N/m g= 9.81 m/s^2