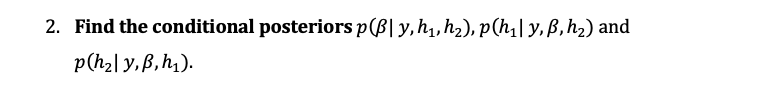Bayesian regression - conditional posteriors

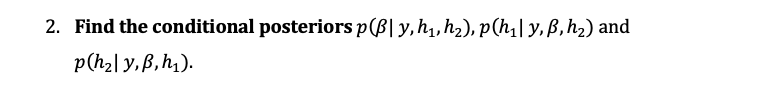
Bayesian Regression Model In order to account for the heteroskedastic pattern in the data, you consider the generalized regression model: Yi = B1 + B2x12 + ... + Brilik + Ei for i = 1, ..., N countries (1) where yi denotes data on the happiness score numbered from 0 (worst) to 10 (best possible life perception) and (342, ..., Xik) denotes data on the following explanatory variables: log GDP per capita, social support, life expectancy, freedom, generosity and corruption so that k = 7. The generalized regression model (1) can be written in matrix form: y= X8+ E vid N (0,2), (2) - with groupwise heteroscedasticity in terms of the precision matrix 5-1 and where you pre sume there are 2 different groups with identical precision parameters hi within each group such that hi 0 0 0 hi 0 hi H = -1 if di = 0 with hi (3) : : The if di = 1 0 0 hi where di is a dummy variable =0 if the country i is an emerging/developing economy and =1 if advanced economy. Assume there is no endogeneity problem in the regression setup (2)-(3) and suppose prior beliefs concerning the unknown parameters of the model 0 = (B', h1, h2)' are represented by the independent Normal-Gamma prior densities: 8 (8,V) (4) h ~ G($1, 41) h2 ~ G(sz?, 12) (5) (6) 2. Find the conditional posteriors p(Bly, hq, hz), p(hily,B, h2) and p(haly,, h). Bayesian Regression Model In order to account for the heteroskedastic pattern in the data, you consider the generalized regression model: Yi = B1 + B2x12 + ... + Brilik + Ei for i = 1, ..., N countries (1) where yi denotes data on the happiness score numbered from 0 (worst) to 10 (best possible life perception) and (342, ..., Xik) denotes data on the following explanatory variables: log GDP per capita, social support, life expectancy, freedom, generosity and corruption so that k = 7. The generalized regression model (1) can be written in matrix form: y= X8+ E vid N (0,2), (2) - with groupwise heteroscedasticity in terms of the precision matrix 5-1 and where you pre sume there are 2 different groups with identical precision parameters hi within each group such that hi 0 0 0 hi 0 hi H = -1 if di = 0 with hi (3) : : The if di = 1 0 0 hi where di is a dummy variable =0 if the country i is an emerging/developing economy and =1 if advanced economy. Assume there is no endogeneity problem in the regression setup (2)-(3) and suppose prior beliefs concerning the unknown parameters of the model 0 = (B', h1, h2)' are represented by the independent Normal-Gamma prior densities: 8 (8,V) (4) h ~ G($1, 41) h2 ~ G(sz?, 12) (5) (6) 2. Find the conditional posteriors p(Bly, hq, hz), p(hily,B, h2) and p(haly,, h)