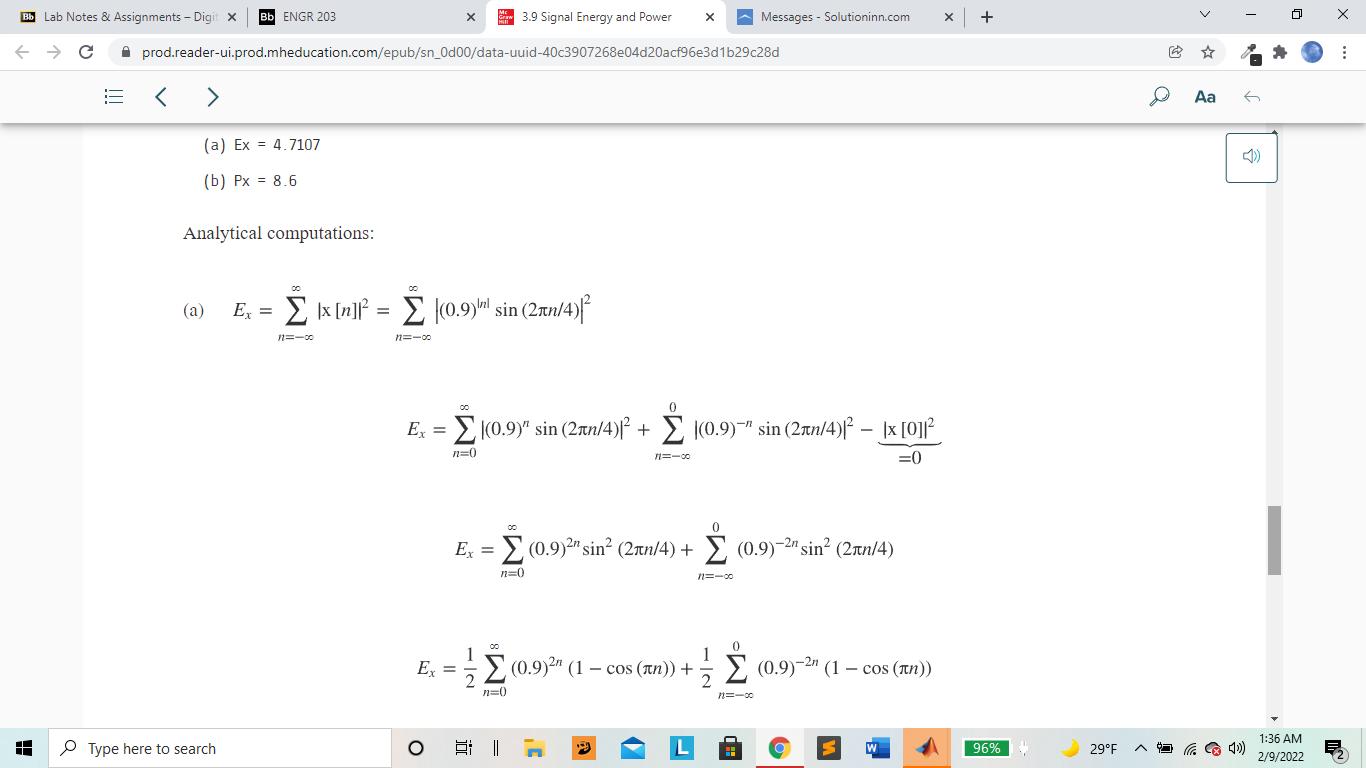
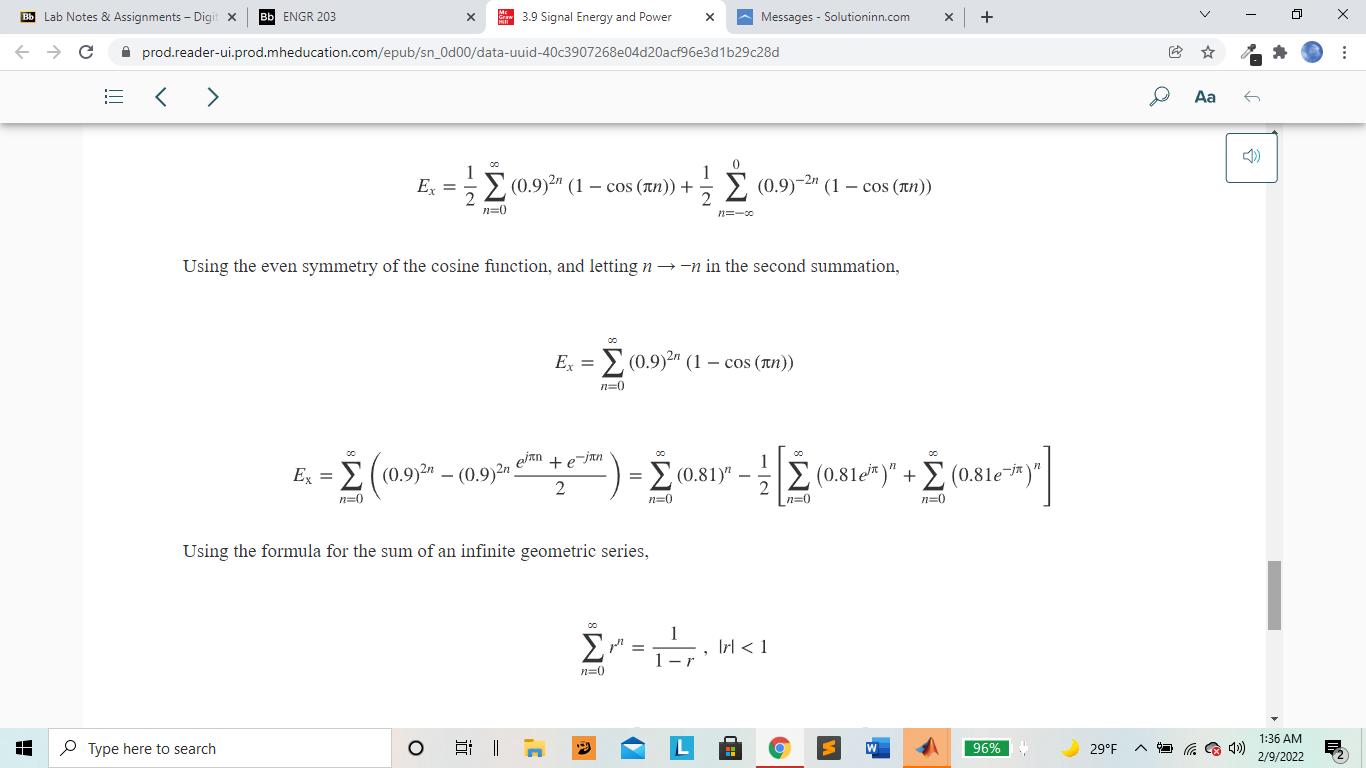
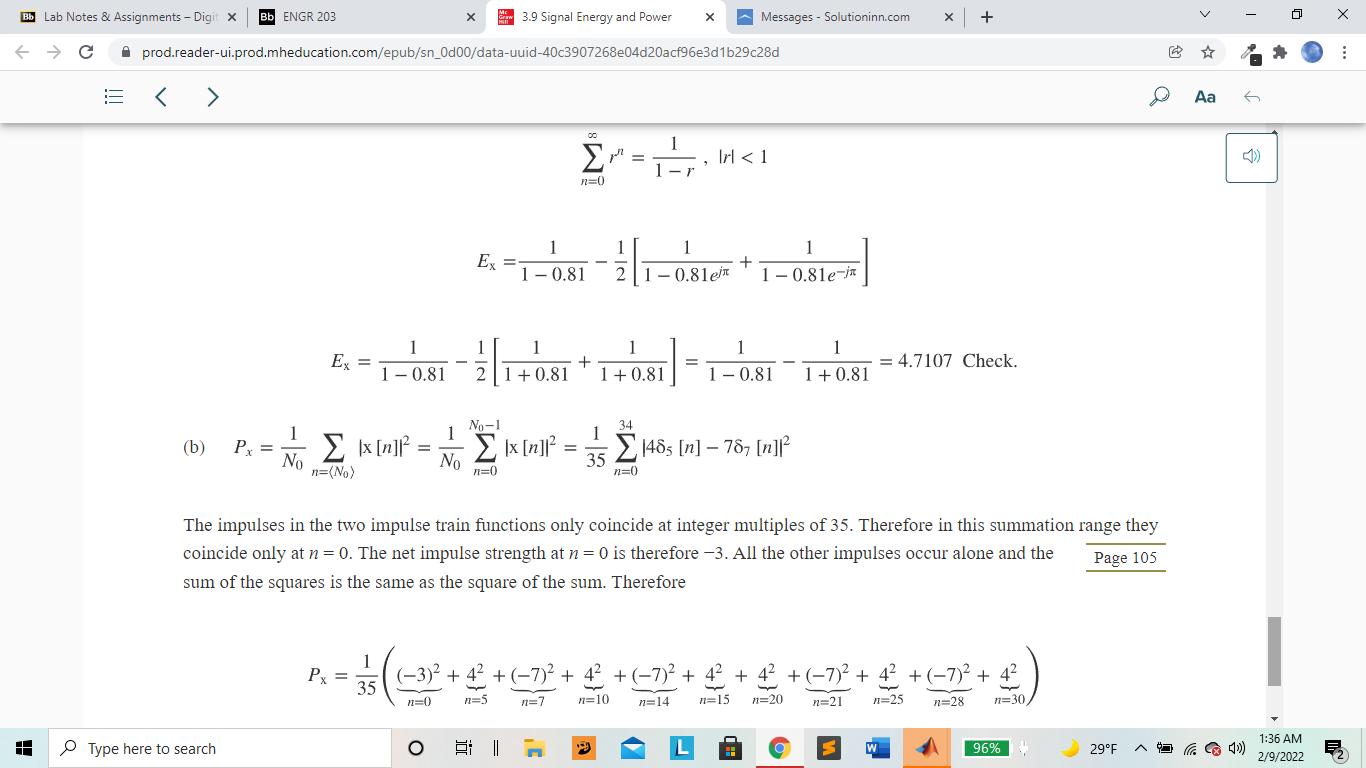
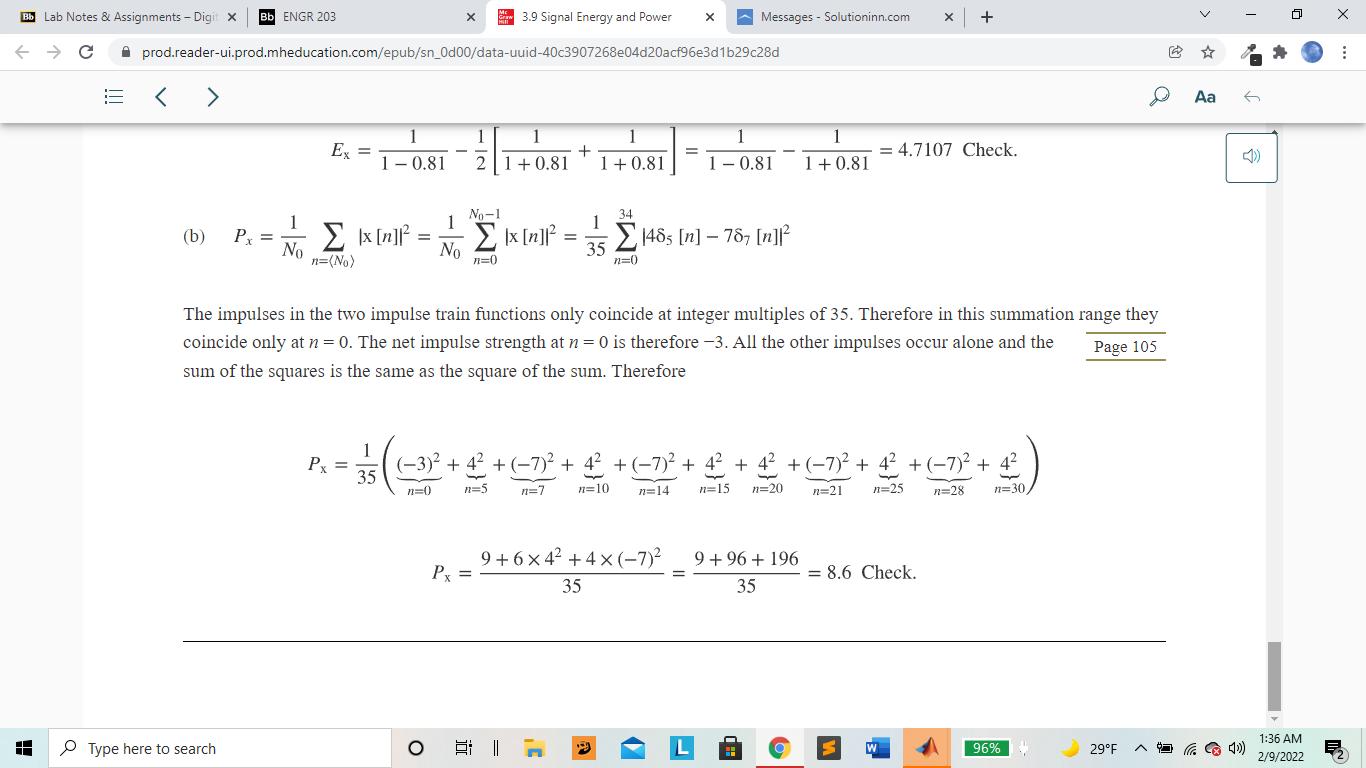
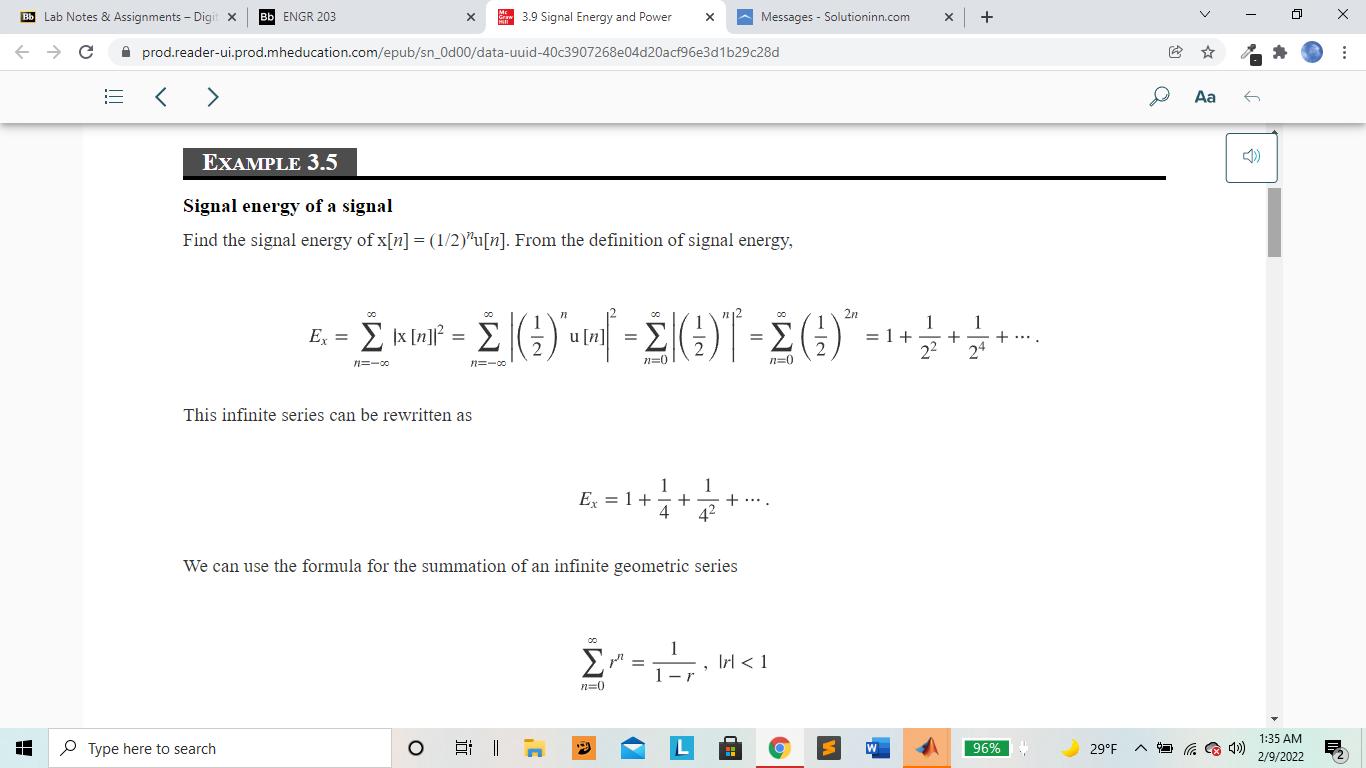
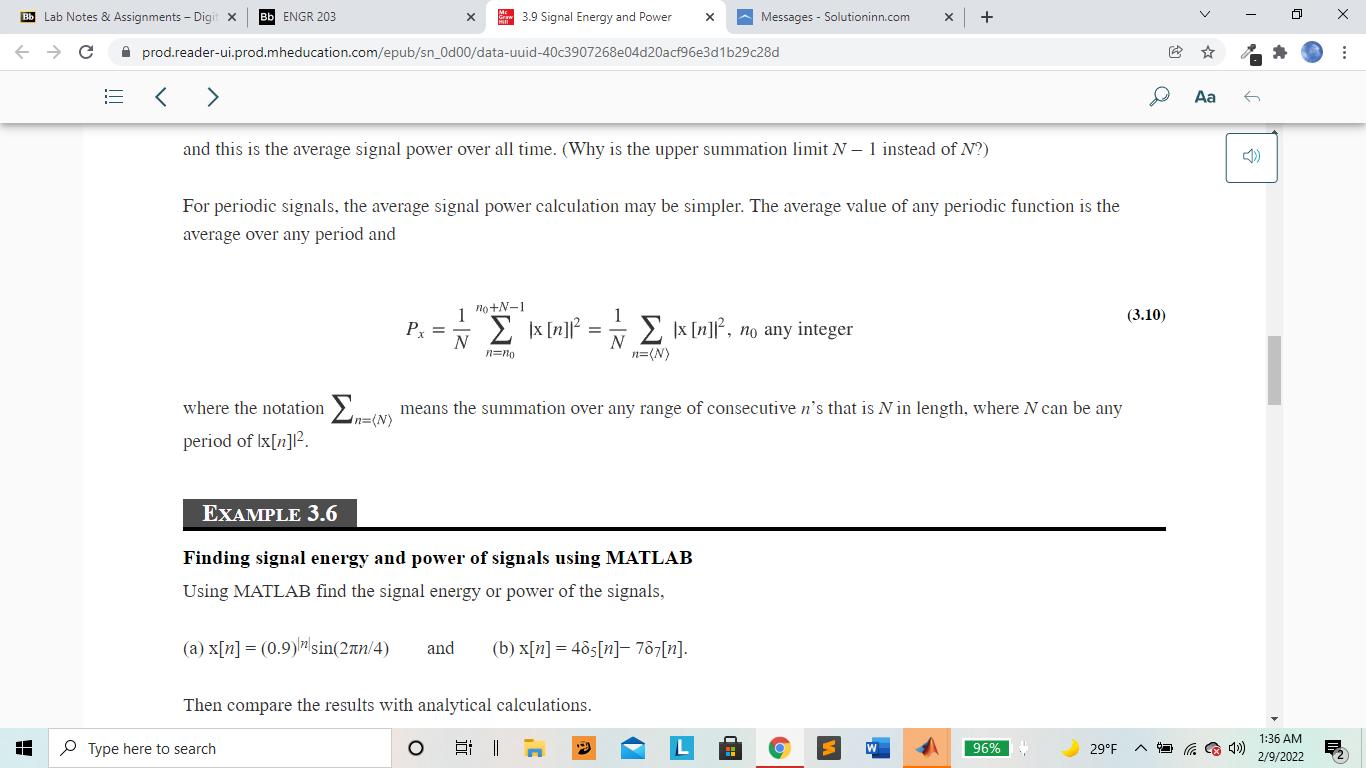
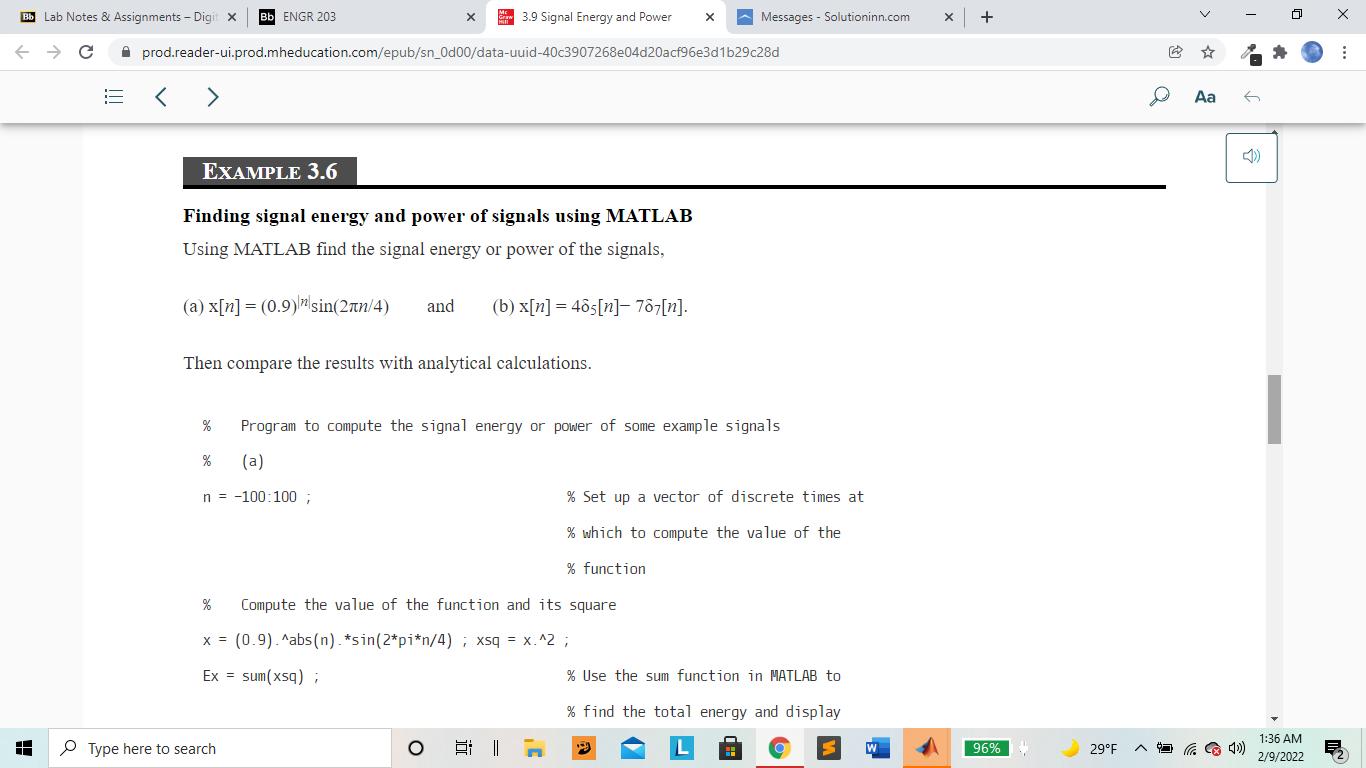
3. Use MATLAB to Calculate (refer to the book, Signals and Systems, Chapter 3.9) signal energy for x1[n] (0 Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C H < > 3.9 SIGNAL ENERGY AND POWER SIGNAL ENERGY Signal energy is defined by Aa Read aloud (3.8) Ex = x[n] 11-00 and its units are simply the square of the units of the signal itself. EXAMPLE 3.5 Signal energy of a signal Find the signal energy of x[n] = (1/2)"u[n]. From the definition of signal energy, Type here to search 96% 29F 1:35 AM 2/9/2022 Bb Lab Notes & Assignments - Digit X Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + C prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d EXAMPLE 3.5 Signal energy of a signal Find the signal energy of x[n] - (1/2)'u[n]. From the definition of signal energy, H 00 Ex = x[n] ] = 11=-00 12=-00 This infinite series can be rewritten as 2n = n=0 1) - = =1+ + 22 24 Ex = 1 + We can use the formula for the summation of an infinite geometric series Type here to search E - Irl < 1 n=0) D Aa 6 2/9/2022 1:35 AM 96% 29F Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C < > H SIGNAL POWER For many signals encountered in signal and system analysis, the summation 00 Ex = x[n] 112=-00 Page 103 D Aa 6 does not converge because the signal energy is infinite, and this usually occurs because the signal is not time limited. The unit sequence is an example of a signal with infinite energy. For signals of this type, it is more convenient to deal with the average signal power of the signal instead of the signal energy. The definition of average signal power is P+ 1 N-1 = lim N00 2N 1x [n] n=-N (3.9) 96% 29F and this is the average signal power over all time. (Why is the upper summation limit N - 1 instead of N?) Type here to search O I 1:35 AM 2/9/2022 Bb Lab Notes & Assignments - Digit X C H Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d > and this is the average signal power over all time. (Why is the upper summation limit N - 1 instead of N?) For periodic signals, the average signal power calculation may be simpler. The average value of any periodic function is the average over any period and no+N-1 1 Px = N N Ix[n]. no any integer n=no n=(N) (3.10) where the notation (N) means the summation over any range of consecutive n's that is N in length, where N can be any period of Ix[n] EXAMPLE 3.6 Finding signal energy and power of signals using MATLAB Using MATLAB find the signal energy or power of the signals, (a) x[n] (0.9) sin(2xn/4) and (b) x[n] = 465[n]- 787[n]. Then compare the results with analytical calculations. Type here to search Aa 6 96% 29F 1:36 AM 2/9/2022 Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C H < > EXAMPLE 3.6 Finding signal energy and power of signals using MATLAB Using MATLAB find the signal energy or power of the signals, (a) x[n] (0.9) sin(2x4) and (b) x[n] = 465[n]- 787[n]. Then compare the results with analytical calculations. % Program to compute the signal energy or power of some example signals % (a) n-100 100 ; % Set up a vector of discrete times at % which to compute the value of the % function % Compute the value of the function and its square x = (0.9). ^abs(n). *sin(2*pi*n/4), xsq = x.^2 ; Ex = sum(xsq); % Use the sum function in MATLAB to % find the total energy and display Type here to search 96% 29F D Aa 6 1:36 AM 2/9/2022 Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C H > > CX 10 use the Sulli TunCCION I PATLAD LU disp(['(b) Ex = ',num2str(Ex)]); % find the total energy and display % the result. % (b) NO = 35; n = 0: NO-1; % The fundamental period is 35 % Set up a vector of discrete times % over one period at which to compute % the value of the function % Compute the value of the function and its square x = 4* impND (5,n) 7*impND (7,n); xsq = x.^2; Px sum(xsq)/NO; % Use the sum function in MATLAB to % find the average power and display % the result. disp(['(d) Px,num2str(Px)]); The output of this program is Type here to search Page 104 96% 29F > Aa 6 1:36 AM 2/9/2022 Bb Lab Notes & Assignments - Digit X C H Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d > (a) Ex = 4.7107 (b) Px = 8.6 Analytical computations: (a) Ex = x[n] === Type here to search 11=-00 11118 (0.9) sin (2n/4) 00 E. (0.9) sin (2/4)| + == n=0 Ex (0.9) sin (2xn/4) - Ix [0]] 11=100 =0 00 Ex=(0.9) sin (2n/4)+ (0.9)- sin (2n/4) n=0 11=100 00 1 n=0 (0.9) (1-cos (n))+ (0.9)-2 (1-cos (xn)) 2 3' N=-00 > Aa 6 Z 96% 29F 1:36 AM 2/9/2022 Bb Lab Notes & Assignments - Digit X C Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d H < > 00 Ex = (0.9) (1 cos (tn)) + (0.9)-2" (1 - cos (n)) n=0 11=100 Using the even symmetry of the cosine function, and letting n -n in the second summation, 00 Ex = (0.9) (1-cos (n)) n=0 einn +e-jan 2 E-((0.9)2- (0.9)2) n=0) 00 00 - (0.81 (0.81)" + (0.81e) n=0 2 n=0 n=0 Using the formula for the sum of an infinite geometric series, Type here to search 3' 00 Irl < 1 n=0 > Aa 6 96% 29F Z 1:36 AM 2/9/2022 Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C < > H Ex = 1 1 -0.81 - 1 00 n=0 Ex 1 -0.81 Irl < 1 r 1 21-0.81e 1 + 1-0.81e-ix 1 1 1 1 1 + = = 4.7107 Check. 21+0.81 1+0.81 1 -0.81 1+0.81 No-1 34 (b) Px No [] 1 1 x [n] No 1485 [n]-787 [n] n=(No) n=0 n=0 > Aa 6 The impulses in the two impulse train functions only coincide at integer multiples of 35. Therefore in this summation range they coincide only at n = 0. The net impulse strength at n = 0 is therefore -3. All the other impulses occur alone and the sum of the squares is the same as the square of the sum. Therefore Page 105 Type here to search n=25 n=28 n=30 (3) + 4 + (-7) + 4 + (7) + 4 + 4 +(-7) + 4 + (-7)+42 1 Px 35 n=0 o n=5 n=7 n=10 n=14 n=15 n=20 n=21 Z 96% 29F 1:36 AM 2/9/2022 Bb ENGR 203 x 3.9 Signal Energy and Power x Messages Solutioninn.com + prod.reader-ui.prod.mheducation.com/epub/sn_0d00/data-uuid-40c3907268e04d20acf96e3d1b29c28d Bb Lab Notes & Assignments - Digit X C H < > 1 1 1 1 1 1 Ex = - + = = 4.7107 Check. 1-0.81 21+0.81 1 +0.81 1 -0.81 1 +0.81 No-1 34 1 (b) Px No |x[n]. 1 No [m] 1 148, [n]-787 [n] 35 n=(No) n=0 n=0 > Aa The impulses in the two impulse train functions only coincide at integer multiples of 35. Therefore in this summation range they coincide only at n = 0. The net impulse strength at n = 0 is therefore -3. All the other impulses occur alone and the sum of the squares is the same as the square of the sum. Therefore Page 105 Type here to search n=25 n=28 n=30 1 (-3) + 4 +(-7) + 4 +(-7) + 4 + 4 + (7) + 4 +(-7) + 4 Px 35 n=0 n=5 n=7 n=10 n=14 n=15 n=20 n=21 9+6x42+4x(-7)2 9+96+ 196 Px = 8.6 Check. 35 35 O 96% 29F D 6 1:36 AM 2/9/2022