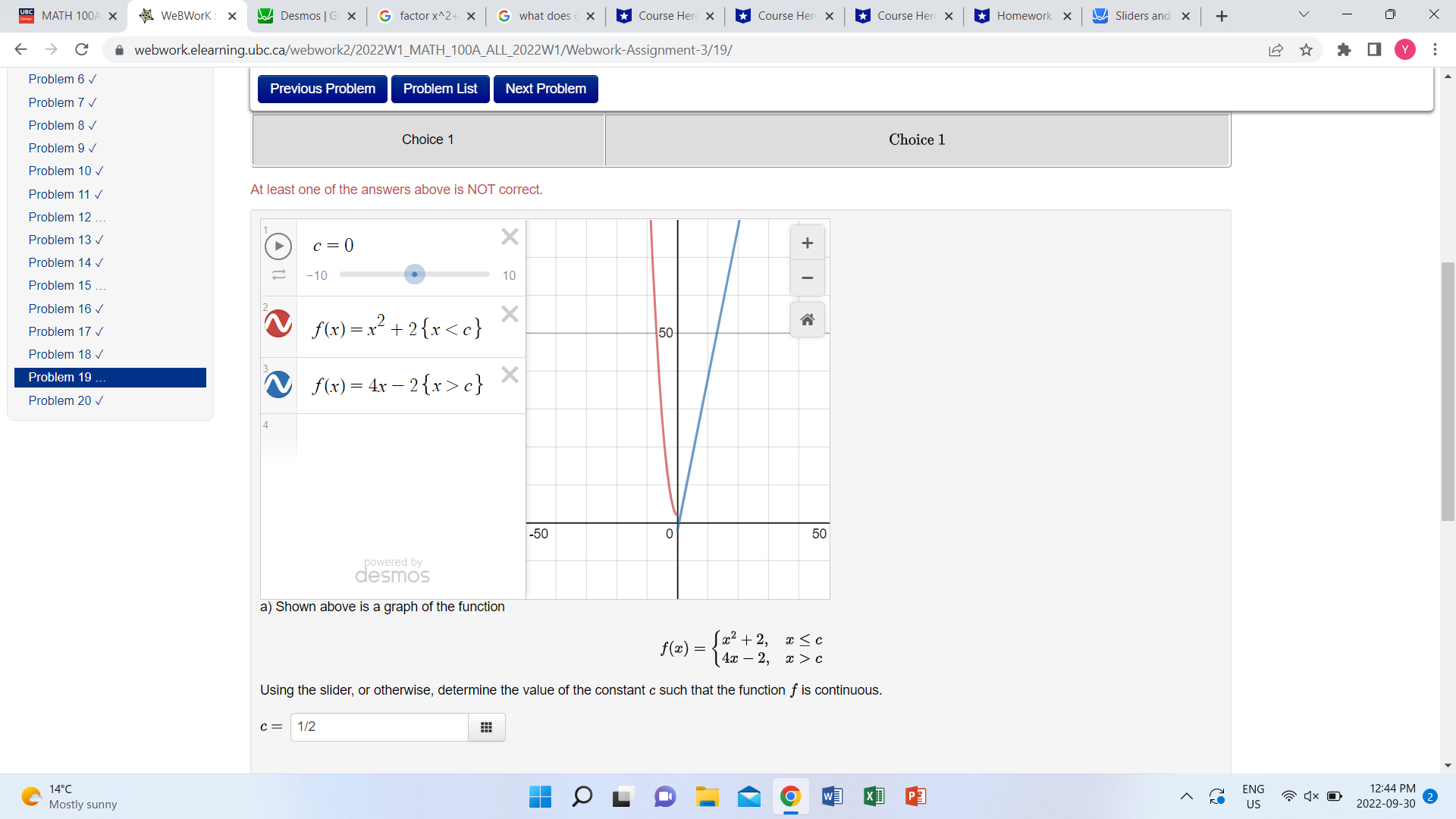
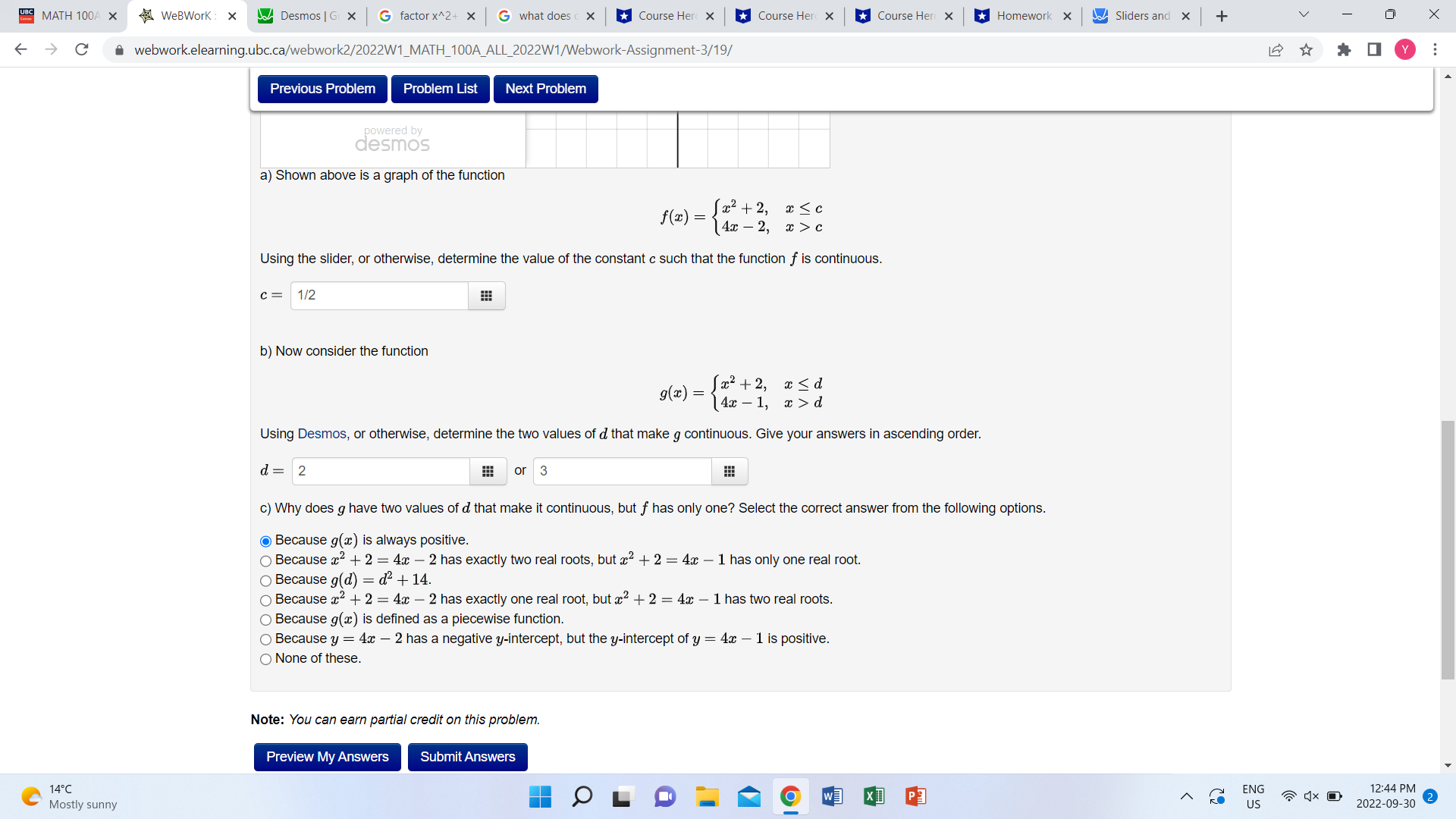
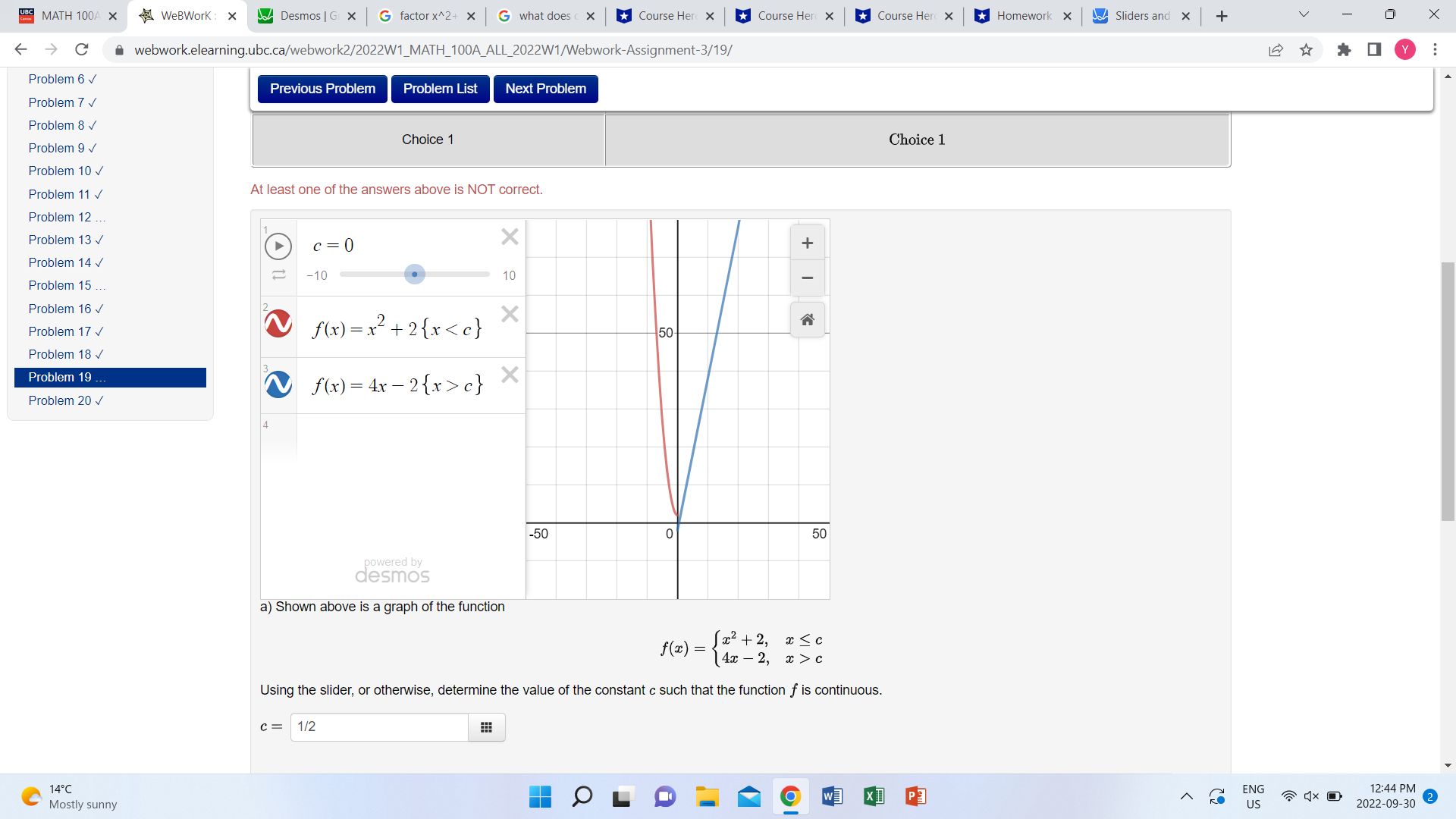
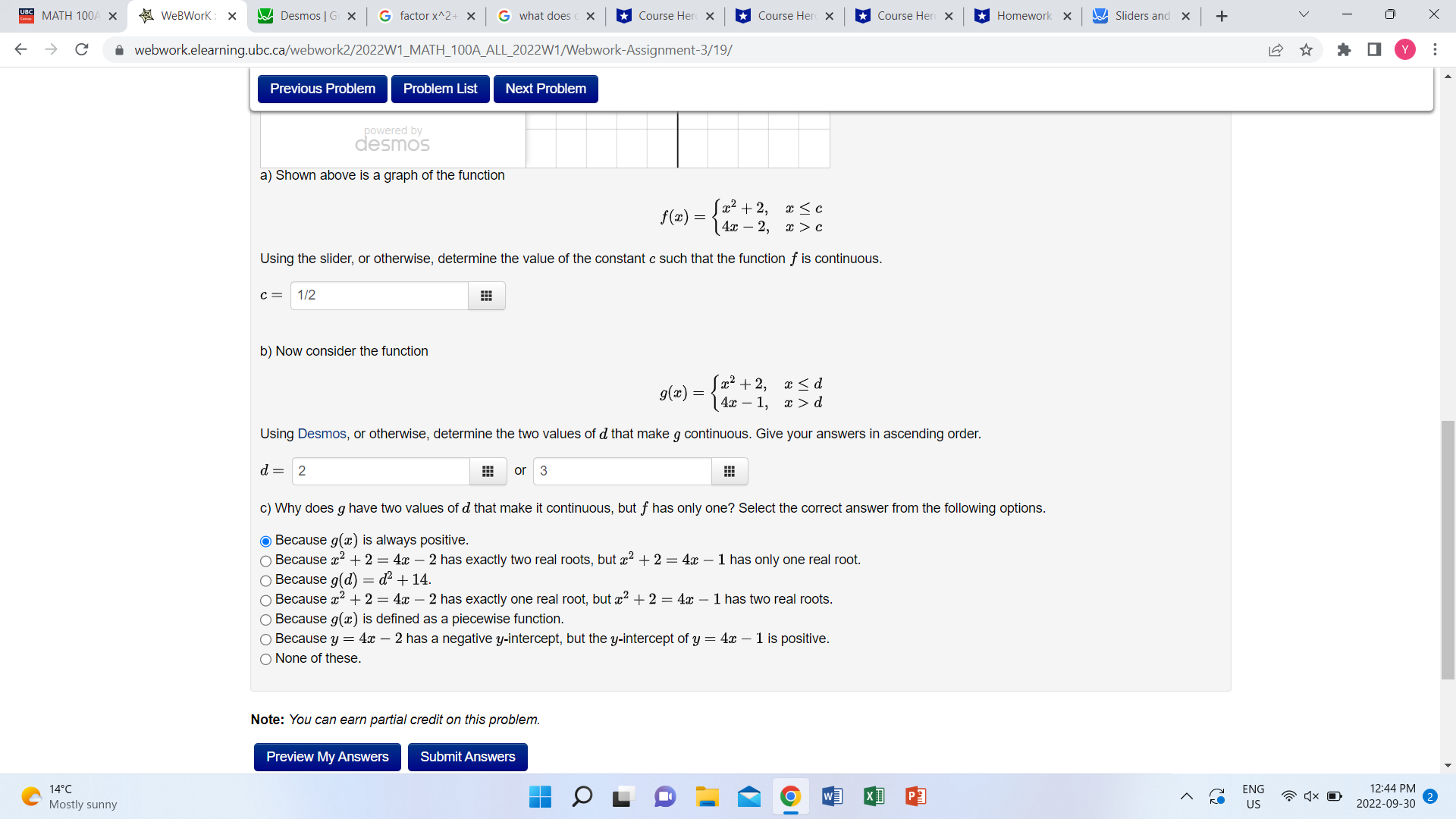
BC MATH 100A X WeBWork : X Desmos | G X G factor x^2+ x G what does c x Course Her( X Course Her X Course Her( X Homework X Sliders and X + V X -> C a webwork.elearning.ubc.ca/webwork2/2022W1_MATH_100A_ALL_2022W1/Webwork-Assignment-3/19/ Problem 6 V Previous Problem Problem List Next Problem Problem 7 v Problem 8 Problem 9 Choice 1 Choice 1 Problem 10 v Problem 11 v At least one of the answers above is NOT correct. Problem 12 ... Problem 13 v C = 0 X Problem 14 -10 10 Problem 15 ... Problem 16 v Problem 17 v ~ f ( x ) = 12+ 2 (x c} X Problem 20 V -50 0 50 powered by desmos a) Shown above is a graph of the function f (2) = 2+2, x5c (4x - 2, x> C Using the slider, or otherwise, determine the value of the constant c such that the function f is continuous. C = 1/2 14 C C Mostly sunny 9 EM ENG 12:44 PM US 2022-09-30 @B MATH 100A X WeBWork : X Desmos | G X G factor x^2+ x G what does c x Course Her( X Course Her X Course Her( X X Homework X Sliders and X + V X > C a webwork.elearning.ubc.ca/webwork2/2022W1_MATH_100A_ALL_2022W1/Webwork-Assignment-3/19/ Previous Problem Problem List Next Problem powered by desmos a) Shown above is a graph of the function f ( 20 ) = 2 + 2, x C Using the slider, or otherwise, determine the value of the constant c such that the function f is continuous. C = 1/2 b) Now consider the function 9 (20 ) = x2+2, asd (4x - 1, x > d Using Desmos, or otherwise, determine the two values of d that make g continuous. Give your answers in ascending order. d = 2 or 3 c) Why does g have two values of d that make it continuous, but f has only one? Select the correct answer from the following options. Because g(x) is always positive. Because x2 + 2 = 4x - 2 has exactly two real roots, but a2 + 2 = 4x - 1 has only one real root. Because g(d) = d' + 14. Because a2 + 2 = 4x - 2 has exactly one real root, but a2 + 2 = 4x - 1 has two real roots. O Because g(x) is defined as a piecewise function. O Because y = 4x - 2 has a negative y-intercept, but the y-intercept of y = 4x - 1 is positive. O None of these. Note: You can earn partial credit on this problem. Preview My Answers Submit Answers 14 C Ed Ix EM ENG 12:44 PM C Mostly sunny US 2022-09-30 @