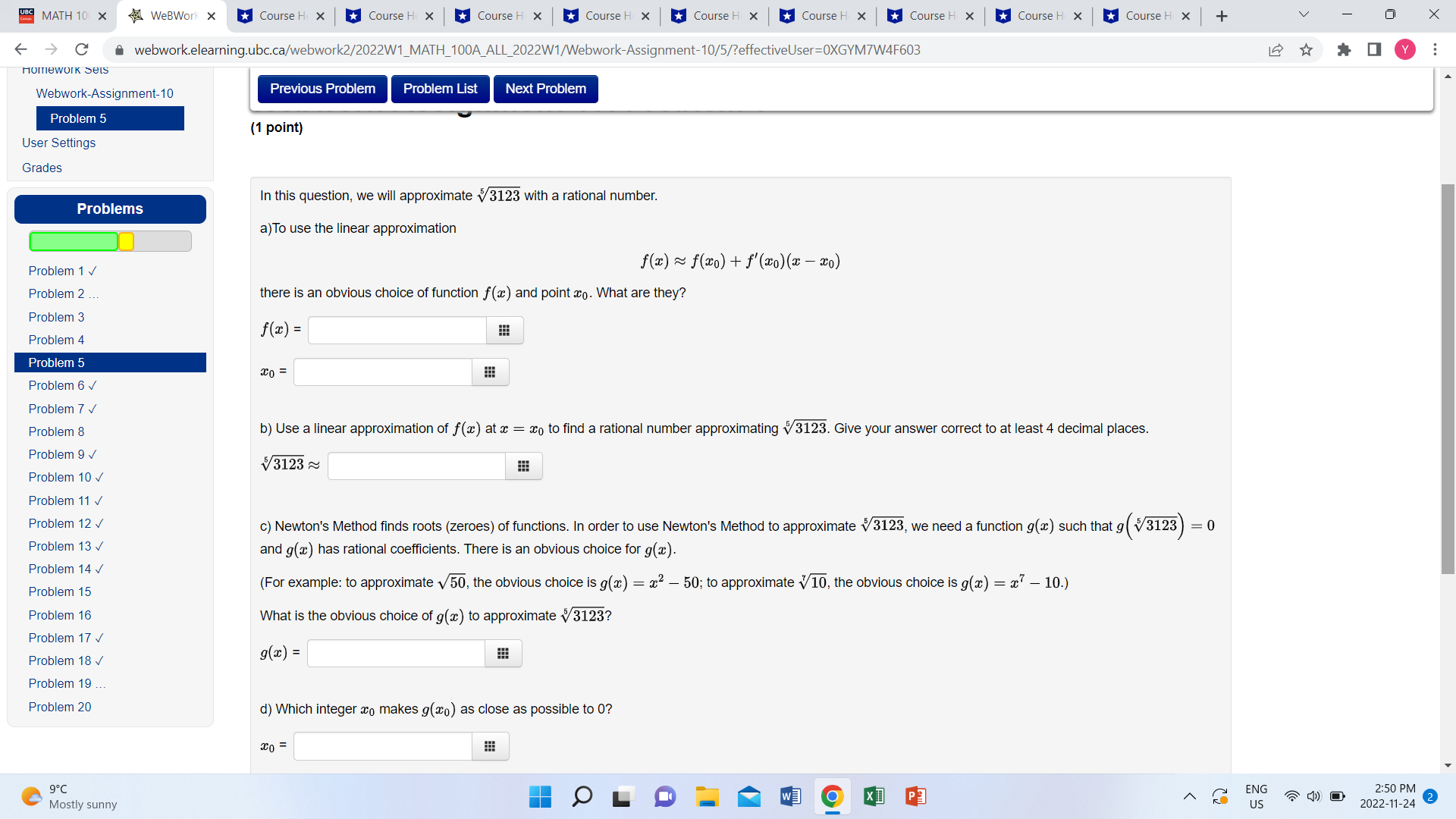
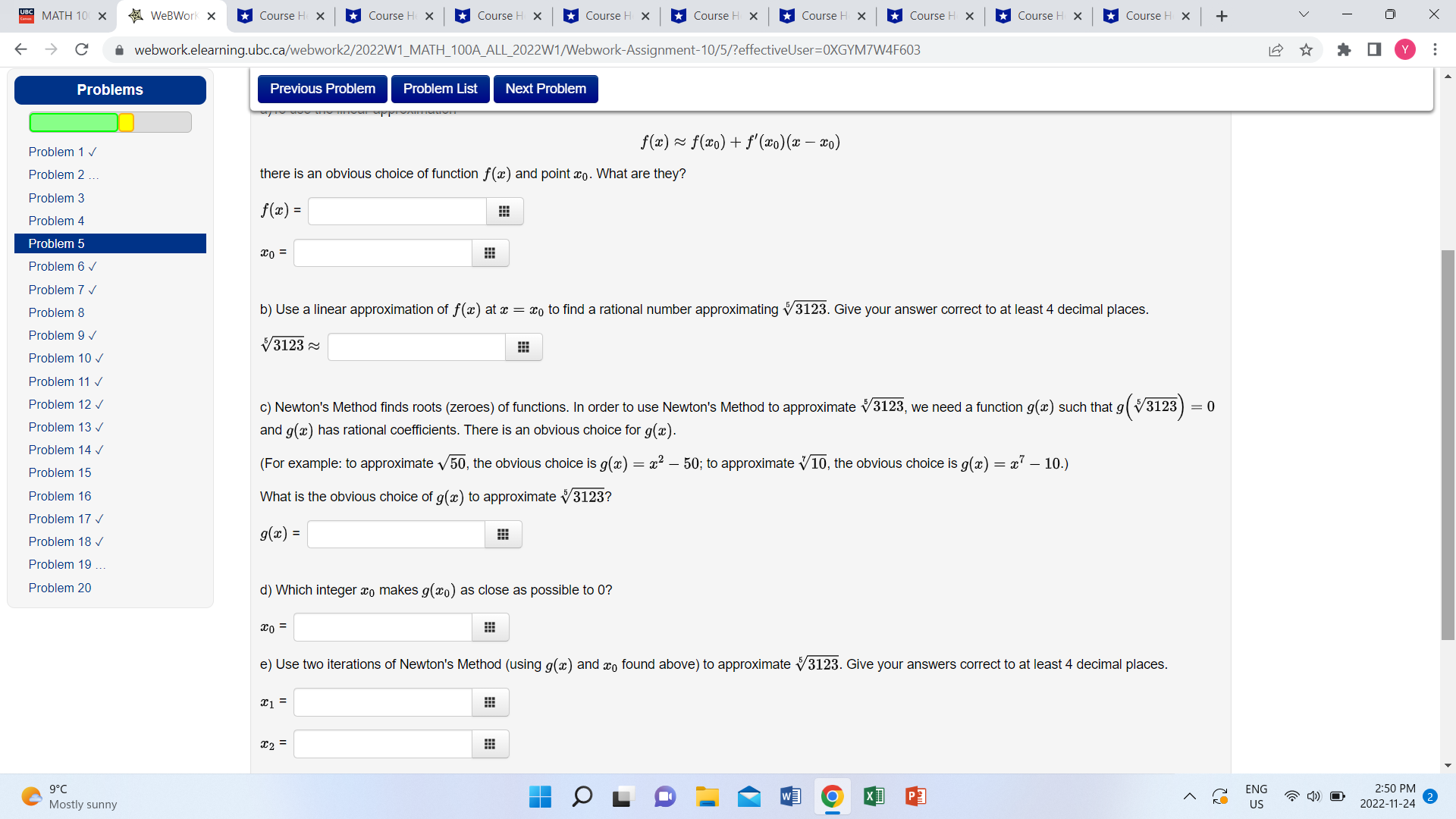
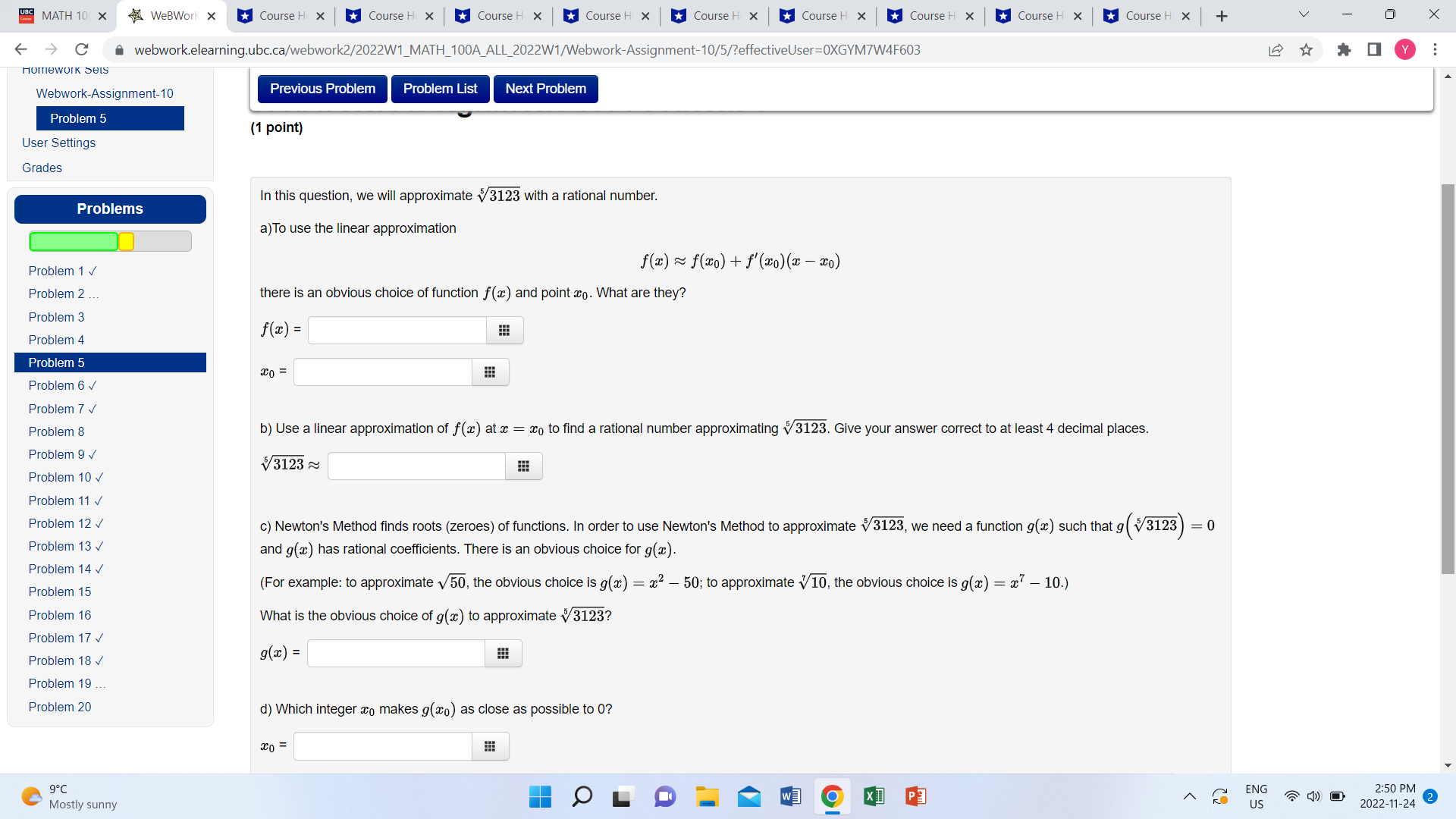
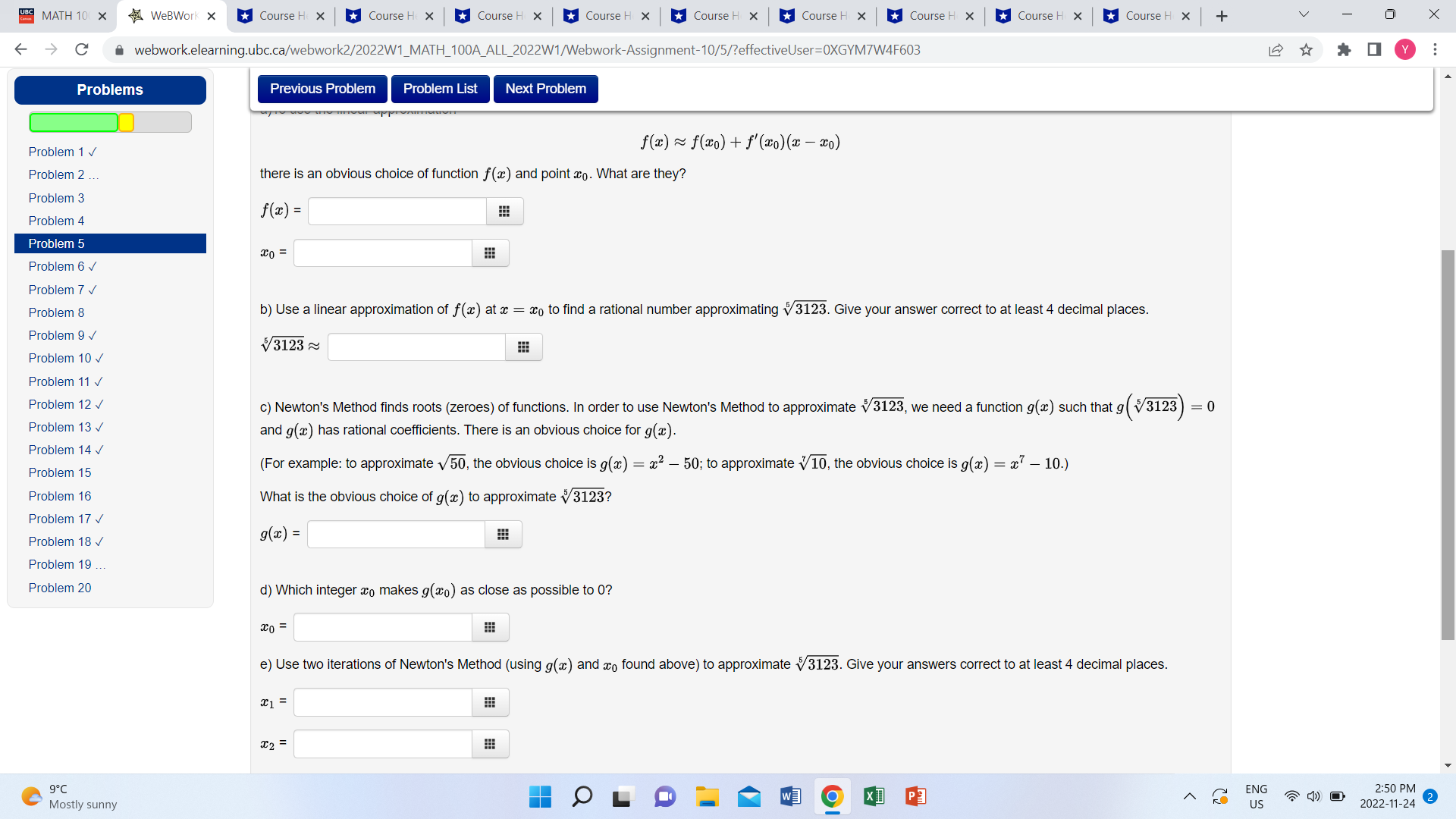
MATH 10( X WeBWork X Course H X Course H X Course H X Course H X Course H X Course H X Course H X Course H X Course H X + V X C a webwork.elearning.ubc.ca/webwork2/2022W1_MATH_100A_ALL_2022W1/Webwork-Assignment-10/5/?effectiveUser=OXGYM7W4F603 Homework Seis Webwork-Assignment-10 Previous Problem Problem List Next Problem Problem 5 (1 point) User Settings Grades In this question, we will approximate v3123 with a rational number. Problems a) To use the linear approximation Problem 1 v f(I) ~ f(xO ) + f'(20)(2 -20) Problem 2 ... there is an obvious choice of function f (@) and point co. What are they? Problem 3 f(z) = Problem 4 Problem 5 0 = Problem 6 v Problem 7 v Problem 8 b) Use a linear approximation of f () at a = aco to find a rational number approximationg v3123. Give your answer correct to at least 4 decimal places. Problem 9 v /3123 ~ Problem 10 Problem 11 v Problem 12 c) Newton's Method finds roots (zeroes) of functions. In order to use Newton's Method to approximate v3123, we need a function g(x) such that g ( $/3123 ) = 0 Problem 13 v and g(x) has rational coefficients. There is an obvious choice for g(a). Problem 14 v Problem 15 (For example: to approximate v50, the obvious choice is g(a) = x2 - 50; to approximate v 10, the obvious choice is g(a) = x - 10.) Problem 16 What is the obvious choice of g(a) to approximate v 3123? Problem 17 v Problem 18 V g(x) = Problem 19 ... Problem 20 d) Which integer co makes g(0) as close as possible to 0? x0 = C 9 . C Mostly sunny w] XI ENG 2:50 PM US 2022-11-24MATH 10( X WeBWork X Course H X Course H X Course H X Course H X Course H X Course H x Course H x Course H X Course H X + V X > C a webwork.elearning.ubc.ca/webwork2/2022W1_MATH_100A_ALL_2022W1/Webwork-Assignment-10/5/?effectiveUser=OXGYM7W4F603 Problems Previous Problem Problem List Next Problem Problem 1 v f(z) ~ f(20) + f'(20) (2 -20) Problem 2 ... there is an obvious choice of function f(@) and point co. What are they? Problem 3 f(z) = Problem 4 Problem 5 x0 = Problem 6 v Problem 7 v Problem 8 b) Use a linear approximation of f () at a = 0 to find a rational number approximationg v3123. Give your answer correct to at least 4 decimal places. Problem 9 /3123 ~ Problem 10 v Problem 11 v Problem 12 V c) Newton's Method finds roots (zeroes) of functions. In order to use Newton's Method to approximate v3123, we need a function g(a) such that g (/3123 ) = 0 Problem 13 v and g(a) has rational coefficients. There is an obvious choice for g(z). Problem 14 V Problem 15 (For example: to approximate v50, the obvious choice is g(a) = x2 - 50; to approximate v10, the obvious choice is g(x) = x7 - 10.) Problem 16 What is the obvious choice of g() to approximate