Before you turn this problem in, make sure everything runs as expected. First, restart the

kernel (in the menubar, select Kernel Restart) and then run all cells (in the menubar, select

Cell Run All).

Make sure you fill in any place that says YOUR CODE HERE or "YOUR ANSWER HERE", as

well as your name and collaborators below:

Problem Statement

In the figure below, is a rigid cube whose sides are of length . , , and are square

plates that are hinged to as shown in the figure.

The motion of the system is such that the angular velocity of in reference frame is:

.

The velocity of point of in the reference frame is:

.

Note that and are time-varying scalars. Further, , , and as shown in the

figure are also time-varying orientation angles.

Your tasks are:

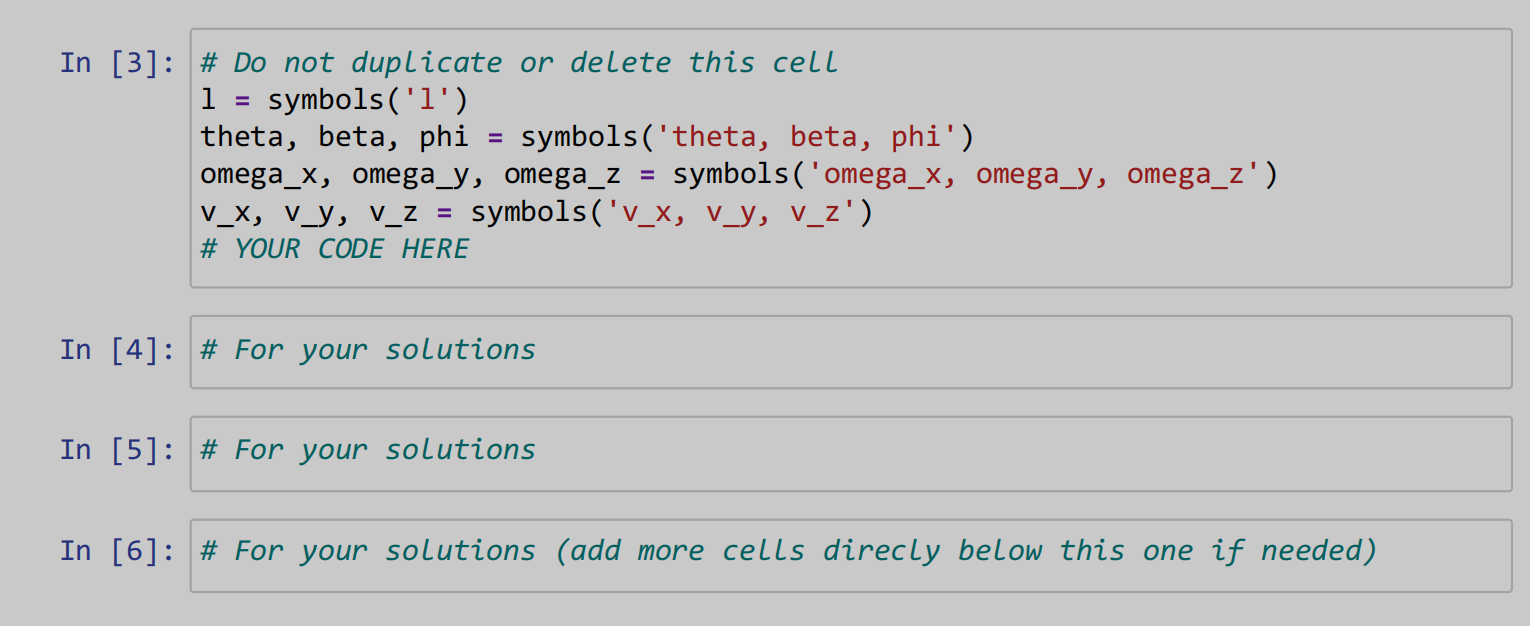
1. Correctly identify which of the scalars are symbols or dynamicsymbols , based on the

above question. You will use these scalars in all subsequent computations. Also, correctly

define all the frames and reference frames using Point and ReferenceFrame from

sympy . (Value: 10 points)

2. Compute : the angular velocity of in . This computation must be stored in the

variable name G_omega_A . (Value: 5 points)

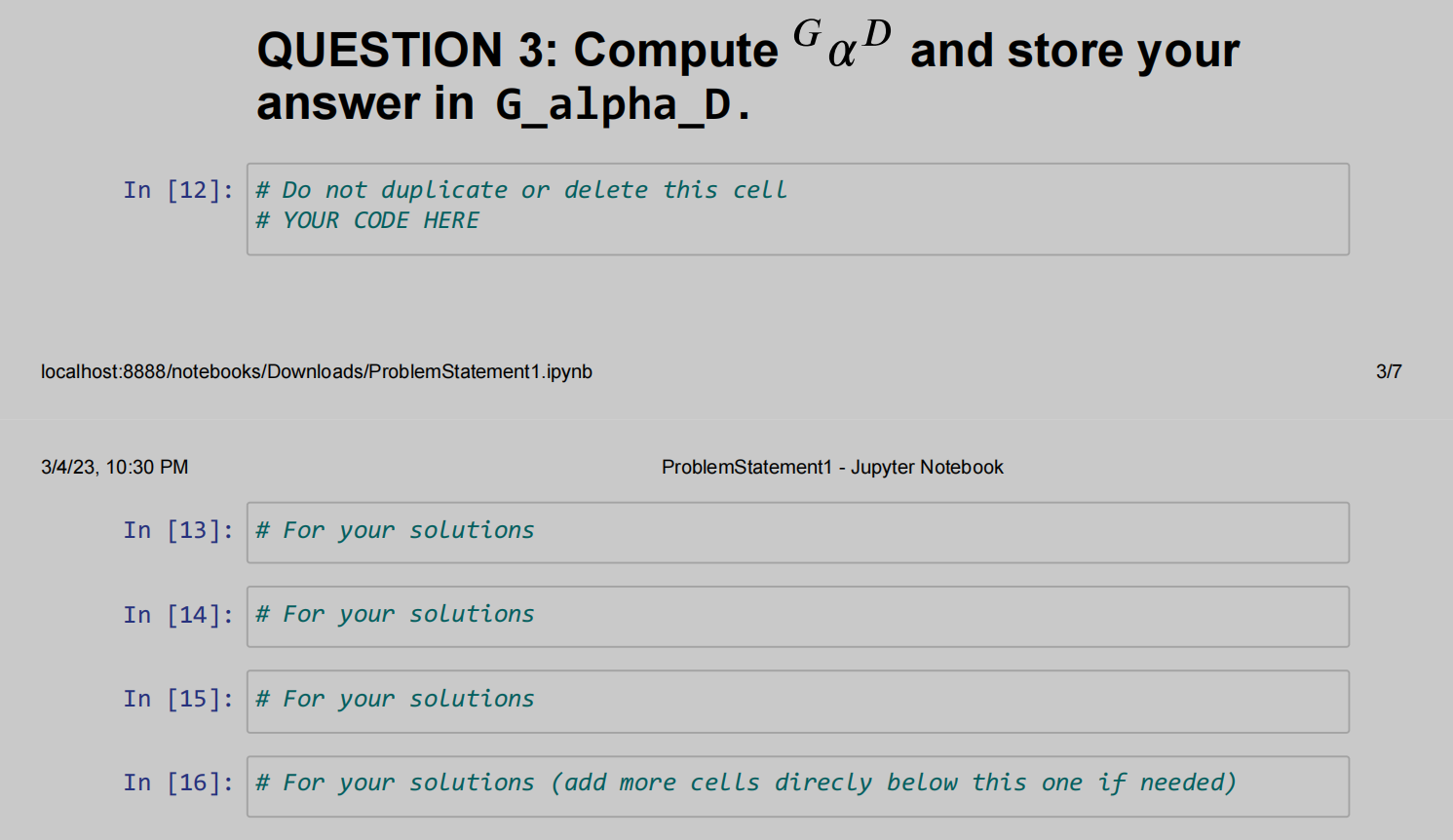
3. Compute : the angular acceleration of in . This computation must be stored in the

variable name G_alpha_D . (Value: 5 points)

4. Compute : the velocity of in . This computation must be stored in the variable

name B_v_Q . (Value: 10 points)

Express all your answers in the

system.

Note: you must make additional variables that follow the above conventions.For example:

1. if any calculations require that you compute then you must create a variable

G_omega_C that saves the value of this vector.

2. if a calculation requires you to compute , then you must save that as a variable using

the convention r_OQ . And so on.

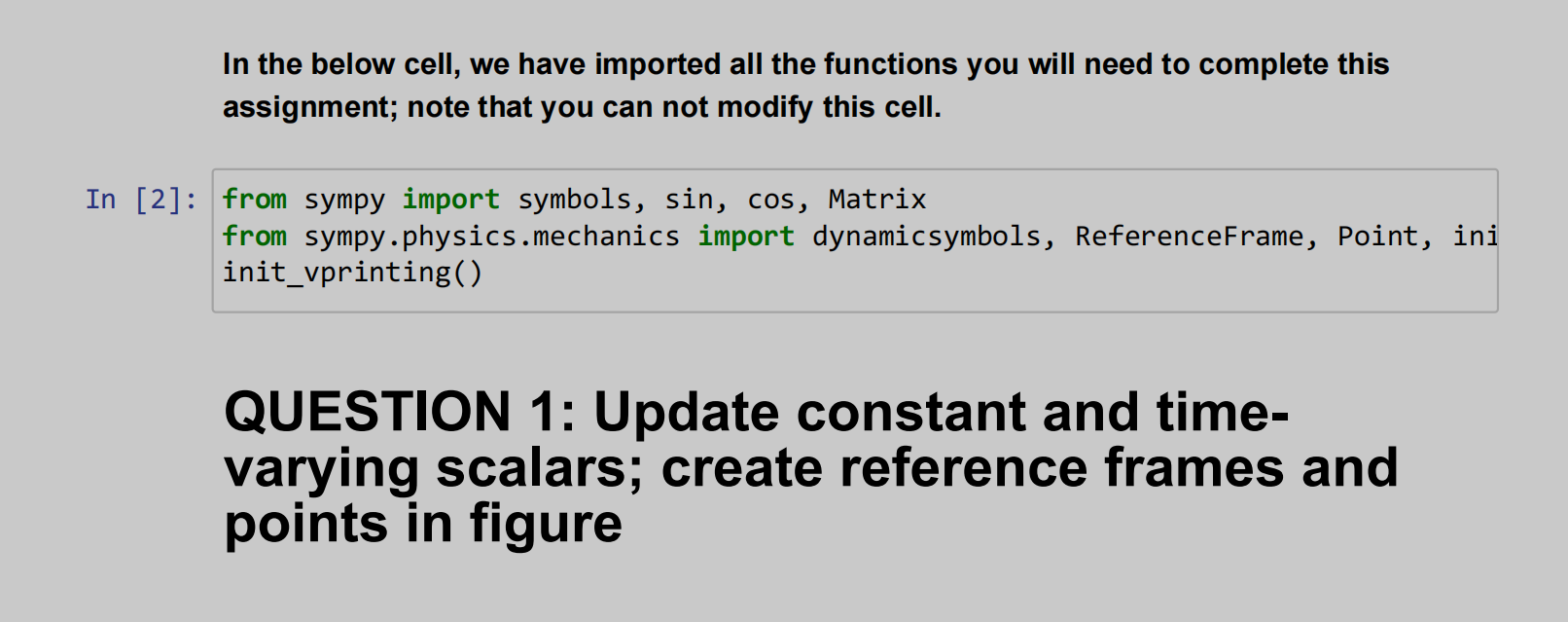
You are provided the code in the cells below that define all the scalar variables as symbols .

Based on the problem statement above, please modify the lines in this first code cell to

correctly identify the scalar variables as constants or time-varying using either symbols or

dynamicsymbols .

Also, in this cell, create all reference frames and points from the figure above using

ReferenceFrame and Point .

In [1]: NAME=""COLLABORATORS="" In the below cell, we have imported all the functions you will need to complete this assignment; note that you can not modify this cell. from sympy import symbols, sin, cos, Matrix from sympy.physics.mechanics import dynamicsymbols, ReferenceFrame, Point, in init_vprinting() QUESTION 1: Update constant and timevarying scalars; create reference frames and points in figure In [3]: \# Do not duplicate or delete this cell 1 = symbols (' 1 ') theta, beta, phi = symbols('theta, beta, phi') omega_x, omega_y, omega_z = symbols('omega_x, omega_y, omega_z') vx,vy,vz=symbols( ' v_x,v_y,vz ' ) \# YOUR CODE HERE In [4]: \# For your solutions In [5]: \# For your solutions In [6]: \# For your solutions (add more cells direcly below this one if needed) QUESTION 2: Compute GA and store your answer in G_omega_A In [7] : In [8]: In [9. In [10]: In [11]: \# For your solutions (add more cells direcly below this one if needed) QUESTION 3: Compute GD and store your answer in G_alpha_D. In [12]: localhost:8888otebooks/Downloads/ProblemStatement1.ipynb 3/4/23,10:30PM ProblemStatement1 - Jupyter Notebook In [13]: In [14]: In [15]: In [16] QUESTION 4: Compute BvQ and store your answer in B_v_Q. In [17]: In [18]: In [19]: In [20] In [21]: \# For your solutions (add more cells direcly below this one if needed) In [1]: NAME=""COLLABORATORS="" In the below cell, we have imported all the functions you will need to complete this assignment; note that you can not modify this cell. from sympy import symbols, sin, cos, Matrix from sympy.physics.mechanics import dynamicsymbols, ReferenceFrame, Point, in init_vprinting() QUESTION 1: Update constant and timevarying scalars; create reference frames and points in figure In [3]: \# Do not duplicate or delete this cell 1 = symbols (' 1 ') theta, beta, phi = symbols('theta, beta, phi') omega_x, omega_y, omega_z = symbols('omega_x, omega_y, omega_z') vx,vy,vz=symbols( ' v_x,v_y,vz ' ) \# YOUR CODE HERE In [4]: \# For your solutions In [5]: \# For your solutions In [6]: \# For your solutions (add more cells direcly below this one if needed) QUESTION 2: Compute GA and store your answer in G_omega_A In [7] : In [8]: In [9. In [10]: In [11]: \# For your solutions (add more cells direcly below this one if needed) QUESTION 3: Compute GD and store your answer in G_alpha_D. In [12]: localhost:8888otebooks/Downloads/ProblemStatement1.ipynb 3/4/23,10:30PM ProblemStatement1 - Jupyter Notebook In [13]: In [14]: In [15]: In [16] QUESTION 4: Compute BvQ and store your answer in B_v_Q. In [17]: In [18]: In [19]: In [20] In [21]: \# For your solutions (add more cells direcly below this one if needed)