Question: Below are the 16 rules to be used for this problem: 1. Natural Deduction III [4 points] a) Using only the 16 basic intro/elim rules

Below are the 16 rules to be used for this problem:

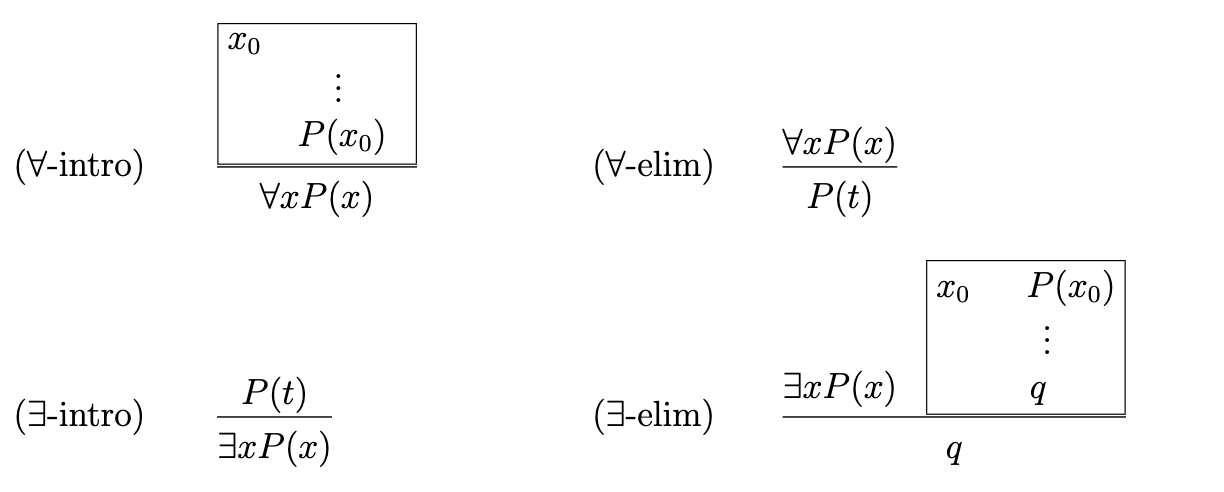
Natural Deduction III [4 points] a) Using only the 16 basic intro/elim rules of Natural Deduction (you may not use logical equivalences), prove that

1. Natural Deduction III [4 points] a) Using only the 16 basic intro/elim rules of Natural Deduction (you may not use logical equivalences), prove that Vx (S(X)^C()] ::. Va [S(x) + C(x)] b) But wait! In Lecture 3 (slides 39 - 41) we said that Va [S(2) ^ C(x)] # V2 [S(x) + C(x)] Show why the converse of (a) does not hold. In particular, use a counterexample to show that it is NOT the case that Vx [S(x) + C(x)] :: Va [S(2) A C(x)] pq pq (1-intro) P 9 pq (1-elim) a (V-intro) T al (V-elim) pVq pva pva r p 9 q (--intro) (+-elim) p+9 9 p 9 9 P 4 q p Ha (H-intro) (H-elim) p Ha 9 p . F (--intro) ( --elim) F (elim) F (F-elim) : P(20) VP(2) (V-intro) (V-elim) VxP() P(t) P(X) : a 3.P(1) (3-intro) P(t) 3xP(x) (3-elim) a 1. Natural Deduction III [4 points] a) Using only the 16 basic intro/elim rules of Natural Deduction (you may not use logical equivalences), prove that Vx (S(X)^C()] ::. Va [S(x) + C(x)] b) But wait! In Lecture 3 (slides 39 - 41) we said that Va [S(2) ^ C(x)] # V2 [S(x) + C(x)] Show why the converse of (a) does not hold. In particular, use a counterexample to show that it is NOT the case that Vx [S(x) + C(x)] :: Va [S(2) A C(x)] pq pq (1-intro) P 9 pq (1-elim) a (V-intro) T al (V-elim) pVq pva pva r p 9 q (--intro) (+-elim) p+9 9 p 9 9 P 4 q p Ha (H-intro) (H-elim) p Ha 9 p . F (--intro) ( --elim) F (elim) F (F-elim) : P(20) VP(2) (V-intro) (V-elim) VxP() P(t) P(X) : a 3.P(1) (3-intro) P(t) 3xP(x) (3-elim) a

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

Super Markets Inc. is considering expanding into the Scottsdale, Arizona, area. You, as director of planning, must present an analysis of the proposed expansion to the operating committee of the...

Below are the 16 rules to be used for this problem: Using only the 16 basic intro/elim rules of Natural Deduction (you may not use logical equivalences), prove that Vx[P(x) + (Q(x) 1 R(x))] EX(-R(3)...

2. The Three Deducteteers (9 points) We're going to use Natural Deduction to prove that Va[-P(x) VQ(x)] = V[P(q) + Q(x)]. a) Using only the 16 basic intro/elim rules of Natural Deduction (you may not...

a) Using only the 16 basic intro/elim rules of Natural Deduction (you may not use logical equivalences), prove that Vx (S(2) AC(2] :: Vx (S(x) + C(x)] b) But wait! In Lecture 3 (slides 39 - 41) we...

I have the following completed: 1120, 2220,1125 A , 1125 E I need the following forms completed asap:SCHEDULE D and G form 4562, form 4797 schedule detail M-1 it should be fairly easy to do the rest...

Please Help me complete this partnership tax return. Attached are the problem and necessary forms, including Form 1065, 1125-A, K-1, 4562, 4797, 8825, 8949, and Schedule B-1 and D of the 1065. 1065...

I could use some assistance on preparing an S Corporation Tax Return. The details are in the attached file. Acct 6113 S Corporation Due Date April 28, 2014 This problem is worth 100 points Prepare...

Not every part of the form need to be filled out. So please read the direction carefully. thank you. Forms to Complete (2015) Form 1065 (not Schedule B) Schedule Dand Forms 8949 Form 1125-A Schedule...

19 Goal is to sketch the curve for f(x) defined as follows { f(x) = [ (In x) / ( sqrt(x))] [NOTE: the implied domain is (x > 0} 1 a) Find the first derivative f(x), and use this to determine all...

Shawn Bates was working to establish a business enterprise with four of his wealthy friends. Each of the five individuals would receive a 20 percent ownership interest in the company. A primary goal...

Good X is exchanged in a competitive market. Which of the following is true if an excise tax is now imposed on the production of good X? (A) If the demand curve is perfectly elastic, the price rises...

Compared with half a century ago, adoption has become _ _ _ _ _ _ _ _ _ common, but it is more open and acceptabl e , so we probably discuss it _ _ _ _ _ _ _ . fill in the blanks more or much less or...

How are Work Breakdown Statements Built and how do they appear in a Project Plan?

What is the most important part of any HCM Project Map and why?

What is the Phase that begins after Project rollover and what activities are part of the Phase?