Below is the solution and sensitivity report from an LP problem for a jeweler that uses silver, gold, and platinum to make custom chains and rings. The output tells the optimal number of chains and rings to produce to maximize profit.

Each chain uses .2 ounces of gold, .3 ounces of silver. Profit per chain is $550.

Each ring uses .15 ounces of gold, .05 ounces of silver, and .05 ounces of platinum. Profit per ring is $400.

The jeweler has 4.1 ounces of gold, 3 ounces of silver, and 1.2 ounces of platinum.

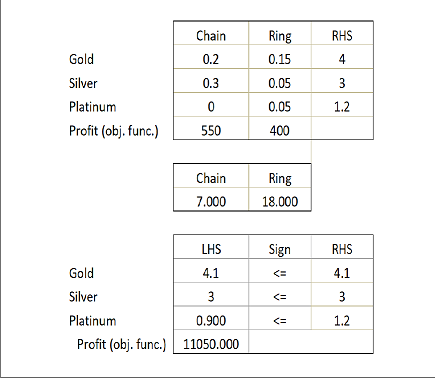
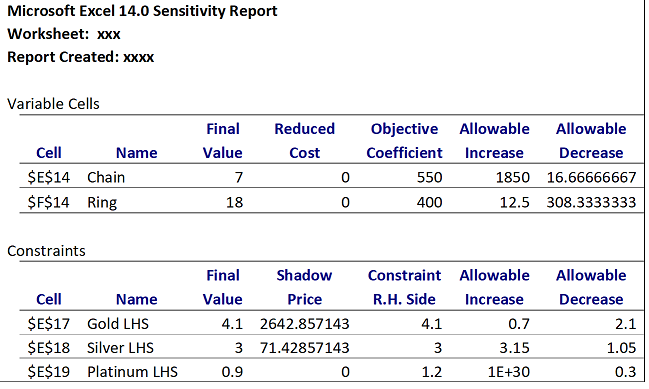
a. The jeweler is considering lowering the price on chains so that the profit per chain would be $500. If she changes the price, would you recommend the she change the number of chains to make? Explain.

b. Suppose the jeweler has access to another .6 ounce of gold. How much would profit increase if she used the extra .60 ounces of gold? Explain

c. Based only on the output above, can you tell how much the jeweler would be willing to pay if another full ounce of gold were available? Explain.

RHS Chain 0.2 Ring 0.15 Gold 4 0.3 3 Silver Platinum Profit (obj. func.) 0.05 0.05 0 1.2 550 400 Chain 7.000 Ring 18.000 LHS Sign RHS 4.1 3 Gold 4.1 Silver 3 Platinum 0.900 Profit (obj. func.) 11050.000 3 1.2 CE Microsoft Excel 14.0 Sensitivity Report Worksheet: xxx Report Created: xxxx Variable Cells Cell Name $E$14 Chain $F$14 Ring Final Value 7 18 Reduced Cost o 0 Objective Allowable Allowable Coefficient Increase Decrease 550 1850 16.66666667 400 12.5 308.3333333 Constraints Cell Name $E$17 Gold LHS $E$18 Silver LHS $E$19 Platinum LHS Final Shadow Value Price 4.1 2642.857143 3 71.42857143 0.9 0 Constraint Allowable R.H. Side Increase 4.1 0.7 3 3.15 1.2 1E+30 Allowable Decrease 2.1 1.05 0.3