Best Route $($Shortest Path$)-$ Revisited

Consider again the Best Route problem from Topic $5.$ The problem is repeated here.

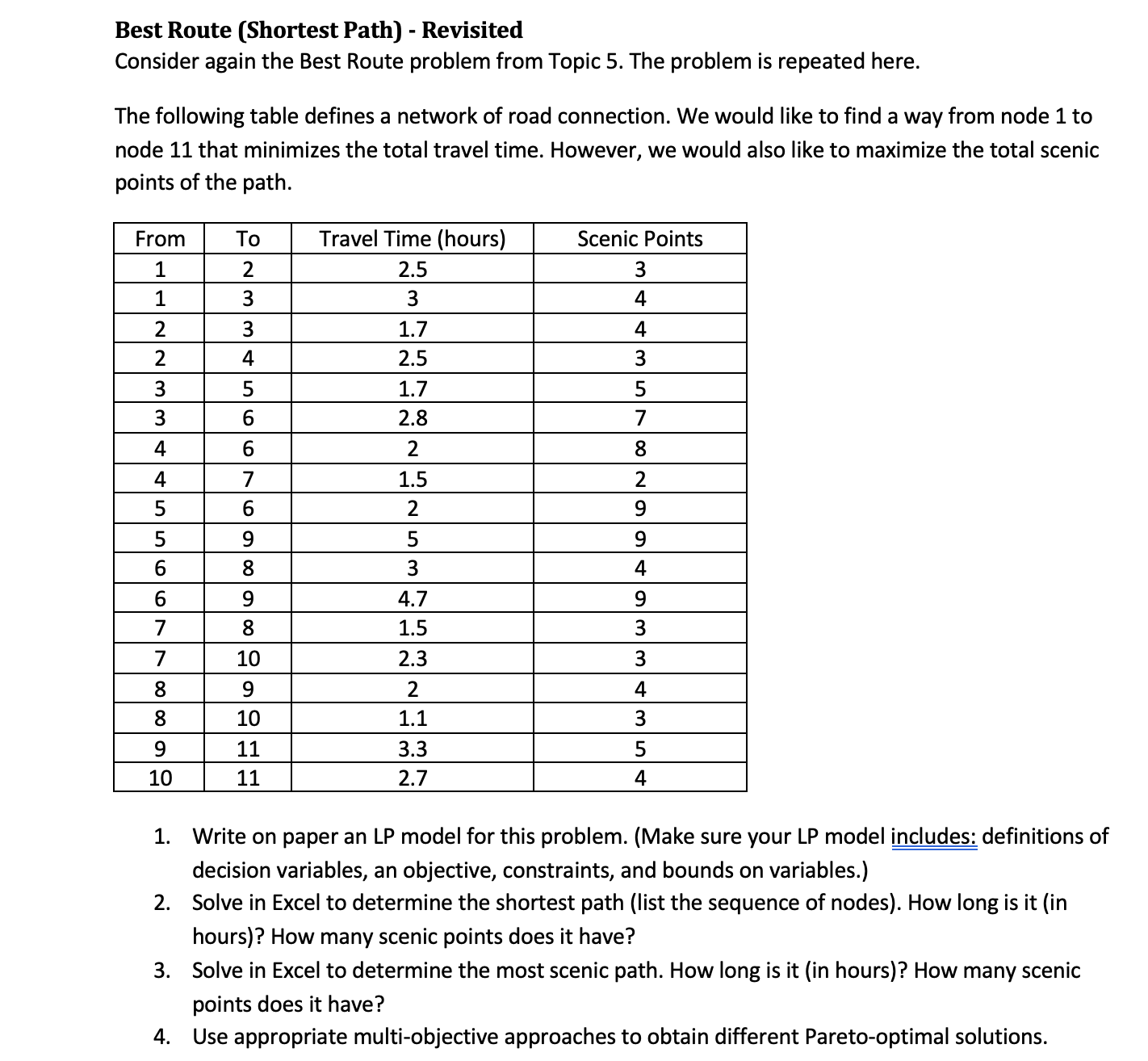
The following table defines a network of road connection. We would like to find a way from node $1$ to node $11$ that minimizes the total travel time. However, we would also like to maximize the total scenic points of the path.

$\backslash$table$[[$From$,$To$,$Travel Time $($hours$),$Scenic Points$],[1,2,2\mathrm{.}5,3],[1,3,3,4],[2,3,1\mathrm{.}7,4],[2,4,2\mathrm{.}5,3],[3,5,1\mathrm{.}7,5],[3,6,2\mathrm{.}8,7],[4,6,2,8],[4,7,1\mathrm{.}5,2],[5,6,2,9],[5,9,5,9],[6,8,3,4],[6,9,4\mathrm{.}7,9],[7,8,1\mathrm{.}5,3],[7,10,2\mathrm{.}3,3],[8,9,2,4],[8,10,1\mathrm{.}1,3],[9,11,3\mathrm{.}3,5],[10,11,2\mathrm{.}7,4]]$

Write on paper an LP model for this problem. $($Make sure your LP model includes: definitions of decision variables, an objective, constraints, and bounds on variables.$)$

Solve in Excel to determine the shortest path $($list the sequence of nodes$).$ How long is it $($in hours$)?$ How many scenic points does it have?

Solve in Excel to determine the most scenic path. How long is it $($in hours$)?$ How many scenic points does it have?

Use appropriate multi$-$objective approaches to obtain different Pareto$-$optimal solutions.