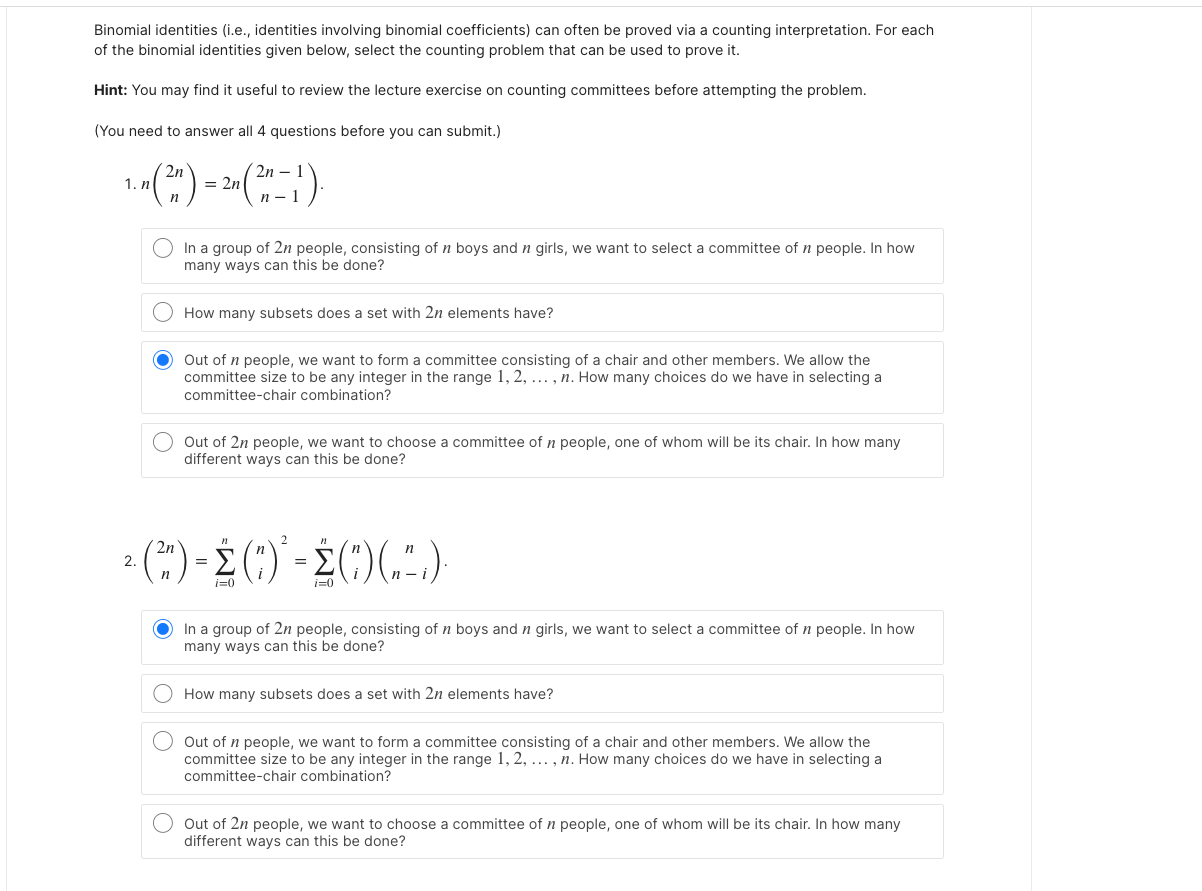
Binomial identities (i.e., identities involving binomial coefficients) can often be proved via a counting interpretation. For each of the binomial identities given below, select the counting problem that can be used to prove it.

Hint: You may find it useful to review the lecture exercise on counting committees before attempting the problem.

(You need to answer all 4 questions before you can submit.)

?(2??)=2?(2??1??1).

In a group of 2? people, consisting of ? boys and ? girls, we want to select a committee of ? people. In how many ways can this be done?

How many subsets does a set with 2? elements have?

Out of ? people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1,2,...,?. How many choices do we have in selecting a committee-chair combination?

Out of 2? people, we want to choose a committee of ? people, one of whom will be its chair. In how many different ways can this be done?

unanswered

(2??)=??=0?(??)2=??=0?(??)(????).

In a group of 2? people, consisting of ? boys and ? girls, we want to select a committee of ? people. In how many ways can this be done?

How many subsets does a set with 2? elements have?

Out of ? people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1,2,...,?. How many choices do we have in selecting a committee-chair combination?

Out of 2? people, we want to choose a committee of ? people, one of whom will be its chair. In how many different ways can this be done?

unanswered

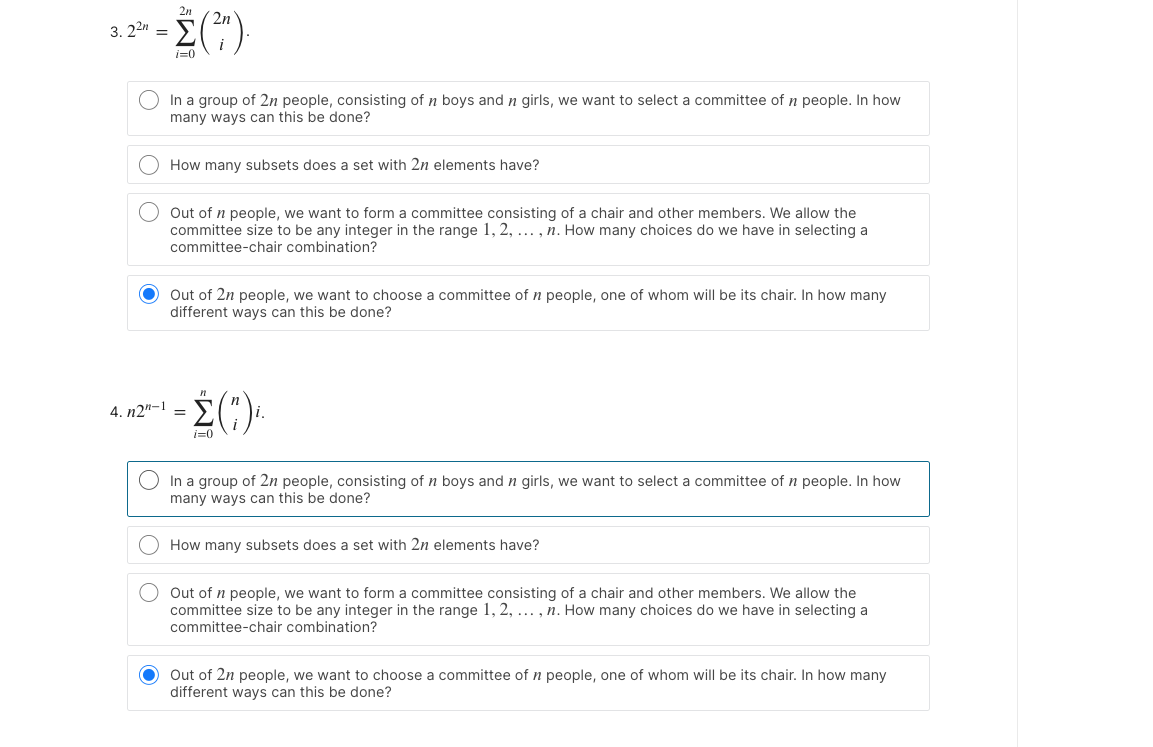
22?=??=02?(2??).

In a group of 2? people, consisting of ? boys and ? girls, we want to select a committee of ? people. In how many ways can this be done?

How many subsets does a set with 2? elements have?

Out of ? people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1,2,...,?. How many choices do we have in selecting a committee-chair combination?

Out of 2? people, we want to choose a committee of ? people, one of whom will be its chair. In how many different ways can this be done?

unanswered

?2??1=??=0?(??)?.

In a group of 2? people, consisting of ? boys and ? girls, we want to select a committee of ? people. In how many ways can this be done?

How many subsets does a set with 2? elements have?

Out of ? people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1,2,...,?. How many choices do we have in selecting a committee-chair combination?

Out of 2? people, we want to choose a committee of ? people, one of whom will be its chair. In how many different ways can this be done?

unanswered

1. 

Binomial identities (i.e., identities involving binomial coefficients) can often be proved via a counting interpretation. For each of the binomial identities given below, select the counting problem that can be used to prove it. Hint: You may find it useful to review the lecture exercise on counting committees before attempting the problem. (You need to answer all 4 questions before you can submit.) 1.}:(2n) = 2n(2n_ 1). n nl O 0 0 (2n 2. it Q) In a group of 2!: people, consisting of :1 boys and n girls, we want to select a committee of :1 people. In how many ways can this be done? How many subsets does a set with 2}: elements have? Out of it people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1, 2, , It. How many choices do we have in selecting a committeechair combination? Out of Zn people, we want to choose a committee of u people, one of whom will be its chair. In how many different ways can this be done? )=3(?)2=(?)(L)- In a group of 2}: people, consisting of in boys and n girls, we want to select a committee of it people. In how many ways can this be done? How many subsets does a set with 2!: elements have? Out of n people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1, 2, , It. How many choices do we have in selecting a committeechair combination? Out of Zn people, we want to choose a committee of u people, one of whom will be its chair. In how many different ways can this be done? 0 it?) In a group of 2!: people, consisting of in boys and :1 girls, we want to select a committee of :1 people. In how many ways can this be clone? How many subsets does a set with 2!: elements have? Out of it people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1, 2, , It. How many choices do we have in selecting a committeechair combination? Out of 2:! people, we want to choose a committee of n people, one of whom will be its chair. In how many different ways can this be clone? man1 = Ems. I i=0 O In a group of 2:: people, consisting of n boys and :1 girls, we want to select a committee of it people. In how many ways can this be clone? O 0 How many subsets does a set with 2!: elements have? Out of it people, we want to form a committee consisting of a chair and other members. We allow the committee size to be any integer in the range 1, 2, , It. How many choices do we have in selecting a committeechair combination? Out of 2:! people, we want to choose a committee of n people, one of whom will be its chair. In how many different ways can this be clone