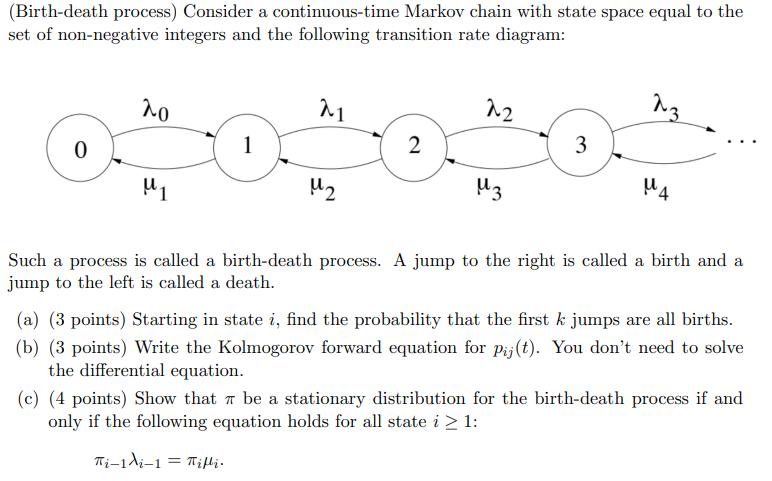
(Birth-death process) Consider a continuous-time Markov chain with state space equal to the set of non-negative integers and the following transition rate diagram: 0 20 M1 21 u2 2 22 3 3 23 4 Such a process is called a birth-death process. A jump to the right is called a birth and a jump to the left is called a death. (a) (3 points) Starting in state i, find the probability that the first k jumps are all births. (b) (3 points) Write the Kolmogorov forward equation for pij(t). You don't need to solve the differential equation. (c) (4 points) Show that be a stationary distribution for the birth-death process if and only if the following equation holds for all state i 1: Ti-1-1= Tifli.