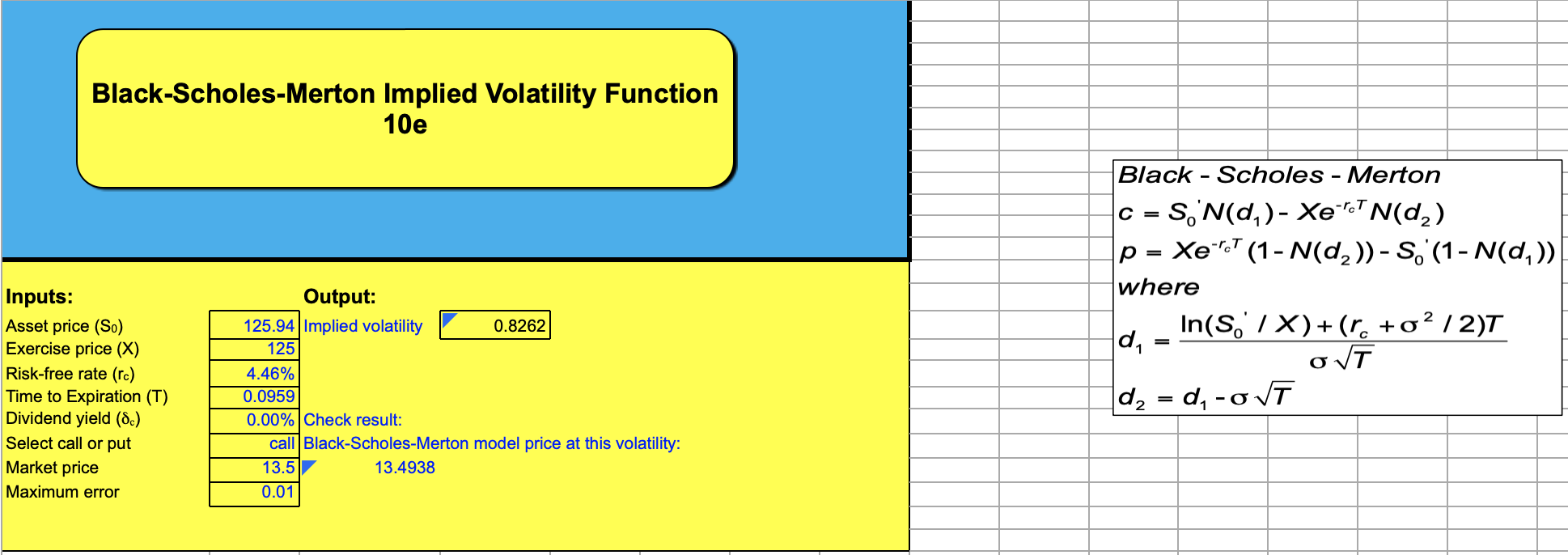
Black-Scholes-Merton Implied Volatility Function 10e Output: Inputs: Asset price (So) Exercise price (X) Risk-free rate (r.) 125.94 Implied volatility 0.8262 125 4.46% Time to Expiration (T) 0.0959 Dividend yield (8.) 0.00% Check result: Select call or put Market price Maximum error call Black-Scholes-Merton model price at this volatility: 13.5 0.01 13.4938 Black - Scholes - Merton c = SN(d)- Xero N(d) C p = Xerc (1- N(d2)) - So' (1 - N(d)) where d In(SIX)+(r +/2)T d = d-oT Today is January 12, 2017. The shares of XYZ Inc. are currently selling for $120 per share. The shares have an estimated volatility of 25%. XYZ Inc. is also expected to pay a dividend of $1.50 with an ex-dividend date of January 25, 2017. The risk-free rate is 6.17 percent per year with continuous compounding. Assume that one call option gives the holder the right to purchase one share. a. Use the Black-Scholes-Merton model to estimate the fair value of a European call option on XYZ shares, with exercise price of $125 and expiration date of March 21, 2017. (Note that 2017 is not a leap year.) b. This European call option has a market price of $3.00. Is it correctly priced? If not, how can an investor use the put-call parity to take advantage of this arbitrage opportunity?