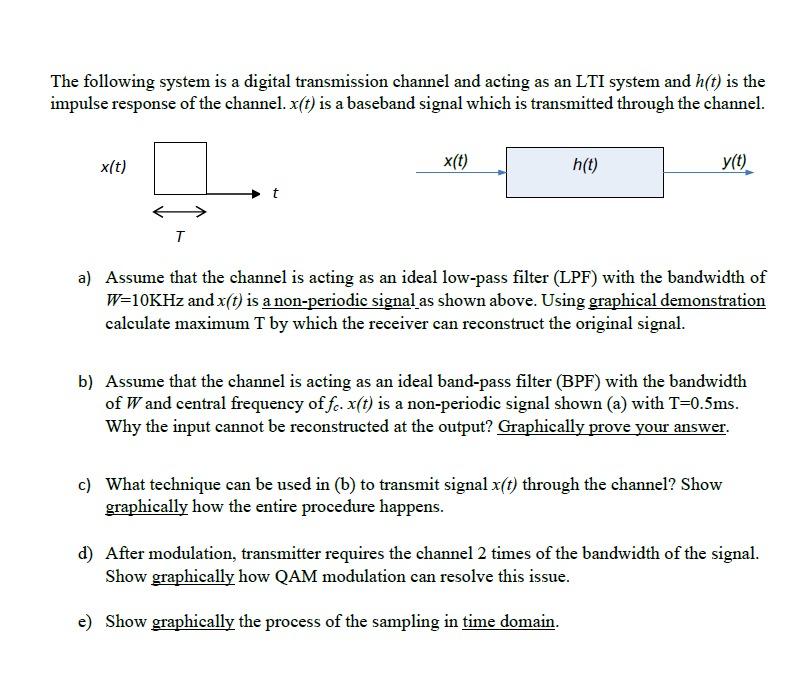
The following system is a digital transmission channel and acting as an LTI system and h(t) is the impulse response of the channel. x(t) is a baseband signal which is transmitted through the channel. x(t) T x(t) h(t) y(t) a) Assume that the channel is acting as an ideal low-pass filter (LPF) with the bandwidth of W=10KHz and x(t) is a non-periodic signal as shown above. Using graphical demonstration calculate maximum T by which the receiver can reconstruct the original signal. b) Assume that the channel is acting as an ideal band-pass filter (BPF) with the bandwidth of W and central frequency of fe. x(t) is a non-periodic signal shown (a) with T=0.5ms. Why the input cannot be reconstructed at the output? Graphically prove your answer. c) What technique can be used in (b) to transmit signal x(t) through the channel? Show graphically how the entire procedure happens. d) After modulation, transmitter requires the channel 2 times of the bandwidth of the signal. Show graphically how QAM modulation can resolve this issue. e) Show graphically the process of the sampling in time domain.