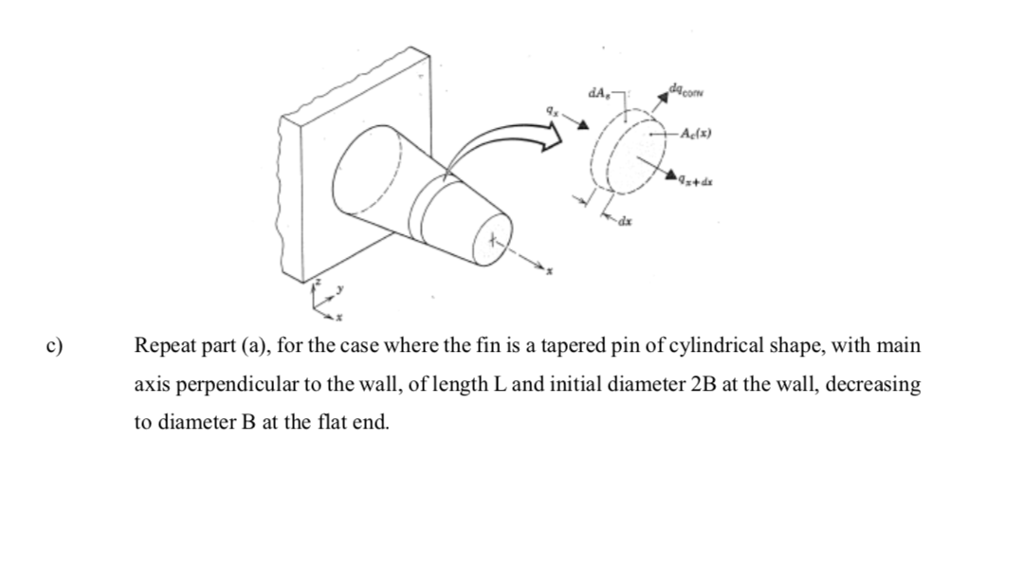
c) dA, dacom -Ac(x) Repeat part (a), for the case where the fin is a tapered pin of cylindrical shape, with main axis perpendicular to the wall, of length L and initial diameter 2B at the wall, decreasing to diameter B at the flat end. Cooling fins are often used to increase area available for heat transfer between metal walls and cooling fluids. For a cylindrical pin fin shown below, it is desired to formulate a simple model for the steady-state temperature in the fin as a function of distance from the wall. The dimension L is much larger than B, so heat loss from the end of the fin can be neglected. The fin is surrounded by a turbulent fluid at temperature Ta, and heat transfer from the curved surface to the fluid is governed by the heat transfer coefficient h W/m K. The thermal conductivity of the fin material is k W/m.K. a) b) Tw -X Ac com 2B By making a shell balance on a suitable control volume, derive a differential equation for the temperature distribution T(x) in the fin. Be careful to state all simplifying assumptions and to show all steps in the derivation. Suggest suitable boundary conditions for the equation you derive. Change your equation and boundary conditions to dimensionless form, by suitably defining a dimensionless space coordinate and a dimensionless temperature 0. Your final equation and conditions should contain only the independent variable, the dependent variable 0, an aspect ratio L/B and a dimensionless group, the combination hB/k, known as the Biot number. The Biot number represents the ratio of the conduction resistance to heat transfer inside the fin (B/k) to the resistance to heat transfer from the fin to its surroundings (1/h).