Question: (c) Use graphical sensitivity analysis to show that if the profit of each kilogram of Deluxe coffee is between $0.4 and $0.6, the current basis

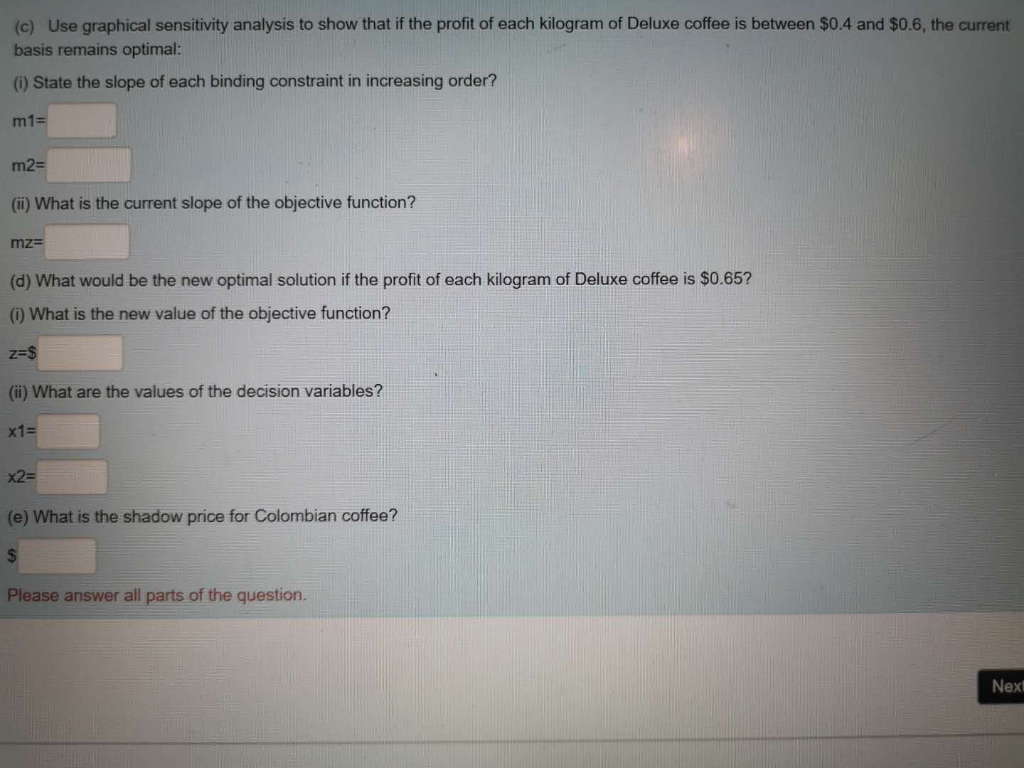
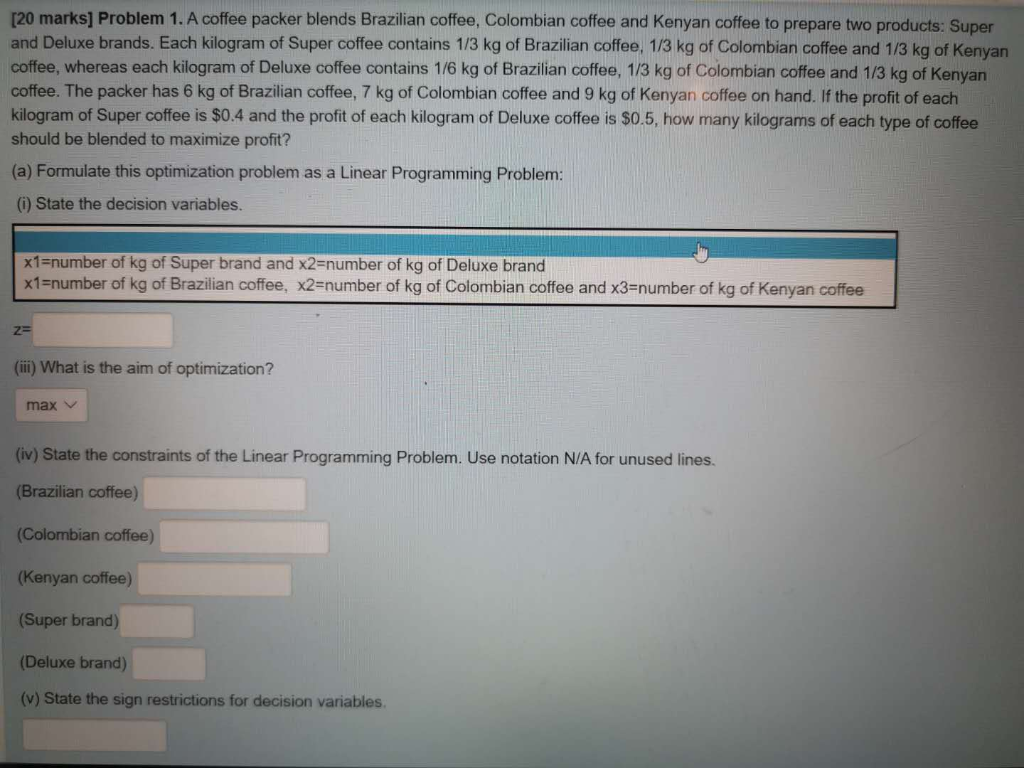
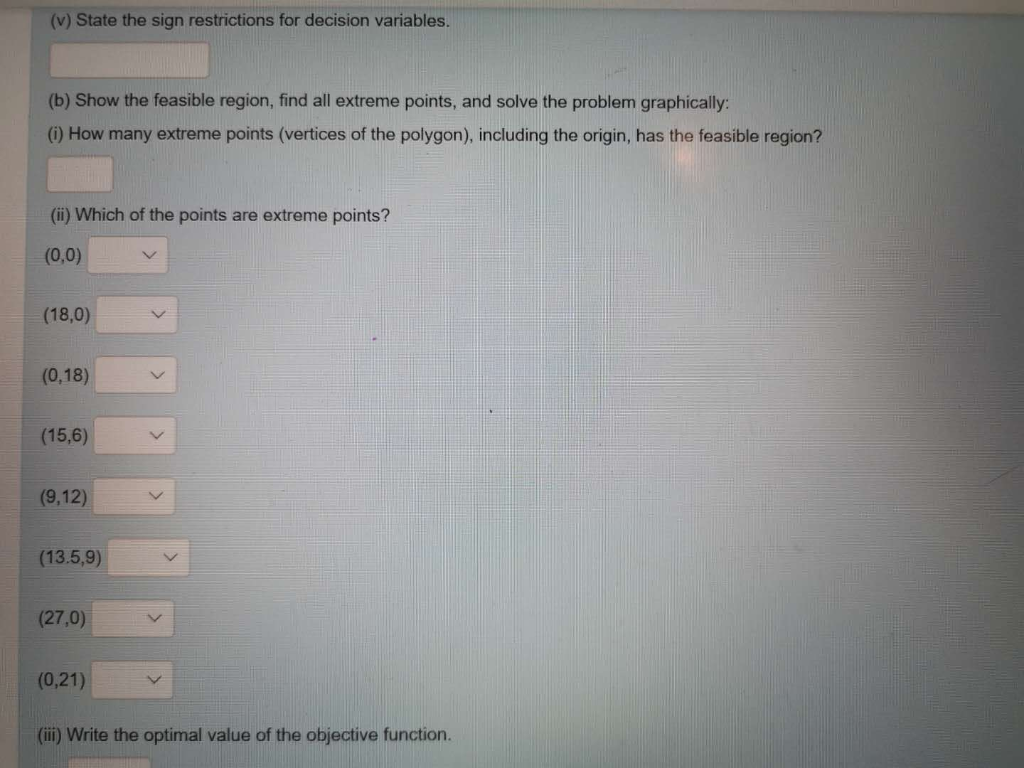
(c) Use graphical sensitivity analysis to show that if the profit of each kilogram of Deluxe coffee is between $0.4 and $0.6, the current basis remains optimal: (i) State the slope of each binding constraint in increasing order? m1= m2= (ii) What is the current slope of the objective function? mz= (d) What would be the new optimal solution if the profit of each kilogram of Deluxe coffee is $0.65? (0) What is the new value of the objective function? z=$ (ii) What are the values of the decision variables? x1 = (e) What is the shadow price for Colombian coffee? Please answer all parts of the question. Next 120 marks] Problem 1. A coffee packer blends Brazilian coffee, Colombian coffee and Kenyan coffee to prepare two products: Super and Deluxe brands. Each kilogram of Super coffee contains 1/3 kg of Brazilian coffee, 1/3 kg of Colombian coffee and 1/3 kg of Kenyan coffee, whereas each kilogram of Deluxe coffee contains 1/6 kg of Brazilian coffee, 1/3 kg of Colombian coffee and 1/3 kg of Kenyan coffee. The packer has 6 kg of Brazilian coffee, 7 kg of Colombian coffee and 9 kg of Kenyan coffee on hand. If the profit of each kilogram of Super coffee is $0.4 and the profit of each kilogram of Deluxe coffee is $0.5, how many kilograms of each type of coffee should be blended to maximize profit? (a) Formulate this optimization problem as a Linear Programming Problem: () State the decision variables. x1=number of kg of Super brand and x2=number of kg of Deluxe brand x1=number of kg of Brazilian coffee, x2=number of kg of Colombian coffee and x3=number of kg of Kenyan coffee Z= (iii) What is the aim of optimization? max (iv) State the constraints of the Linear Programming Problem. Use notation N/A for unused lines. (Brazilian coffee) (Colombian coffee) (Kenyan coffee) (Super brand) (Deluxe brand) (v) State the sign restrictions for decision variables. (v) State the sign restrictions for decision variables. (b) Show the feasible region, find all extreme points, and solve the problem graphically: (i) How many extreme points (vertices of the polygon), including the origin, has the feasible region? (ii) Which of the points are extreme points? (0,0) (18,0) (0,18) (15,6) (9,12) (13.5,9) (27,0) (0,21) (ii) Write the optimal value of the objective function. (c) Use graphical sensitivity analysis to show that if the profit of each kilogram of Deluxe coffee is between $0.4 and $0.6, the current basis remains optimal: (i) State the slope of each binding constraint in increasing order? m1= m2= (ii) What is the current slope of the objective function? mz= (d) What would be the new optimal solution if the profit of each kilogram of Deluxe coffee is $0.65? (0) What is the new value of the objective function? z=$ (ii) What are the values of the decision variables? x1 = (e) What is the shadow price for Colombian coffee? Please answer all parts of the question. Next 120 marks] Problem 1. A coffee packer blends Brazilian coffee, Colombian coffee and Kenyan coffee to prepare two products: Super and Deluxe brands. Each kilogram of Super coffee contains 1/3 kg of Brazilian coffee, 1/3 kg of Colombian coffee and 1/3 kg of Kenyan coffee, whereas each kilogram of Deluxe coffee contains 1/6 kg of Brazilian coffee, 1/3 kg of Colombian coffee and 1/3 kg of Kenyan coffee. The packer has 6 kg of Brazilian coffee, 7 kg of Colombian coffee and 9 kg of Kenyan coffee on hand. If the profit of each kilogram of Super coffee is $0.4 and the profit of each kilogram of Deluxe coffee is $0.5, how many kilograms of each type of coffee should be blended to maximize profit? (a) Formulate this optimization problem as a Linear Programming Problem: () State the decision variables. x1=number of kg of Super brand and x2=number of kg of Deluxe brand x1=number of kg of Brazilian coffee, x2=number of kg of Colombian coffee and x3=number of kg of Kenyan coffee Z= (iii) What is the aim of optimization? max (iv) State the constraints of the Linear Programming Problem. Use notation N/A for unused lines. (Brazilian coffee) (Colombian coffee) (Kenyan coffee) (Super brand) (Deluxe brand) (v) State the sign restrictions for decision variables. (v) State the sign restrictions for decision variables. (b) Show the feasible region, find all extreme points, and solve the problem graphically: (i) How many extreme points (vertices of the polygon), including the origin, has the feasible region? (ii) Which of the points are extreme points? (0,0) (18,0) (0,18) (15,6) (9,12) (13.5,9) (27,0) (0,21) (ii) Write the optimal value of the objective function

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

Hello, I need help with this question A company produces two products A and B. The sales volume for A is at least 30% of the total sales of both A and B. However the company can not sell more than...

A farmer plans to mix two types food to make a mix of low cost feed for animals in his farm. A bag of food A costs $10 and contains 40 units of protein, 20 units of minerals and 10 units of vitamins....

f Sugareo is considering making Type 4 andy bars. A Type 4 cundy har earns 17% profit and requires 3 oz of sugar and 4oz of chocolate. Should Sugarco manufacture any 'Type 4 candy bars? 7 The...

Amy Lloyd is interested in leasing a new car and has contacted three automobile dealers for pricing information. Each dealer offered Amy a closed-end 36 month lease with no down payment due at the...

Problem 13-08 (Algorithmic) The following payoff table shows the profit for a decision problem with two states of nature and two decision alternatives: State of Nature Decision Alternative S2 51 6 d...

Consider the following linear programming problem P with three resources and three activities: Maximize Z = 4 x 1 + 3 x 2 + 6 x 3 (0) subject to 2 x 1 + 5 x 2 + 9 x 3 500 (1) 4 x 1 + 5 x 3 350 (2) 2...

uantitative Analysis BA 452 Homework 3 Questions Homework 3 covers the theory and applications in Lessons I-6 and I-7. This document has four parts: Objectives of doing your homework. Assignment of...

Suppose that you are given a decision situation with three possible states of nature: S1, S2, and S3. The prior probabilities are P(S1) = 0.22, P(S2) = 0.59, and P($3) = 0.19. With sample information...

Question 7: Sensitivity analysis (20 marks, 2 marks per subquestion) A garden store prepares various grades of pine bark for mulch: nuggets ( x 1 ), mini-nuggets ( x 2 ), and chips ( x 3 ). The...

Part II: Sensitivity analysis (10 marks, 2 marks per subquestion) A garden store prepares various grades of pine bark for mulch: muggets (x1),mini nuggets (c), and chips (x3). The production process...

Study Table 61 , Table 62, and review the chapter text describing how the indirect cost is allocated. This assignment will change the allocation bases input for (A) Number of Visits (Volume), (B)...

Lisa Harcourt sat at her desk and could not believe the feedback received from the recent employee survey. As HR director for Top Notch Storage, she has always thought that the company had highly...

Rent paid to the building's owners should be credited to A building owner's account B rent account C cash account D expense account

Choose the terms that most appropriately complete the following statements. The terms can be used more than once. 1. When a product or service does not conform to customer expectations in terms of...