Calc2:

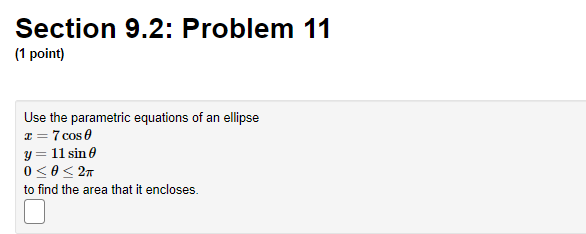
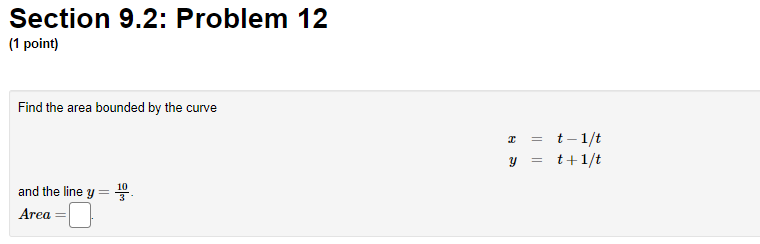
Section 9.2: Problem 10 (1 point) Consider the parametric equation I = 15(cos # + 0 sin 0) y = 15(sin 0 - 8 cos 0) What is the length of the curve for 0 = 0 to 0 = 11Section 9.2: Problem 11 (1 point) Use the parametric equations of an ellipse I = 7 cos 0 1 = 11 sine to find the area that it encloses.Section 9.2: Problem 12 {1 point} Find The area hounded by The curve tut t+1ft and the line y = E. Arm=D. 3 Section 9.2: Problem 6 (1 point) Use a graph to estimate the coordinates of the highest point and the leftmost point on the curve x = 9tel, y = 5te-t. Then find the exact coordinates. Highest point: Leftmost point: The curve has one horizontal asymptote and one vertical asymptote. Find them. Horizontal asymptote: y = Vertical asymptote: I =