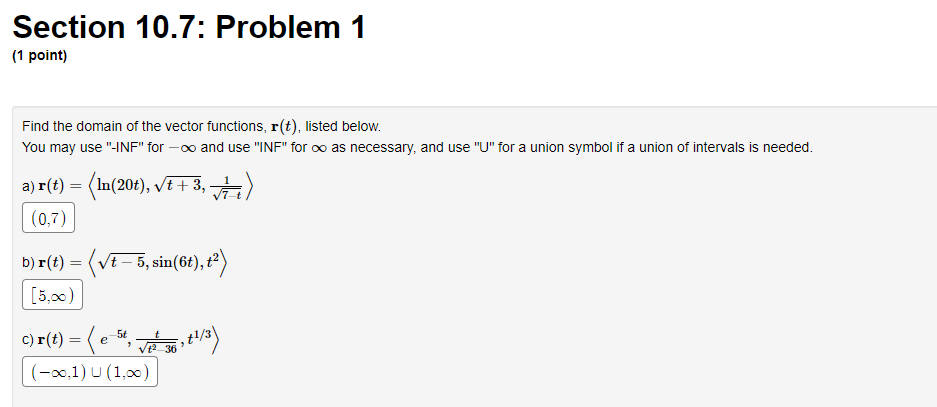
Question: Calculus 3: Section 10.7: Problem 1 [1 point} Find the domain of the 1vector functions, rm. listed below. You may use INF for oo and
Calculus 3:

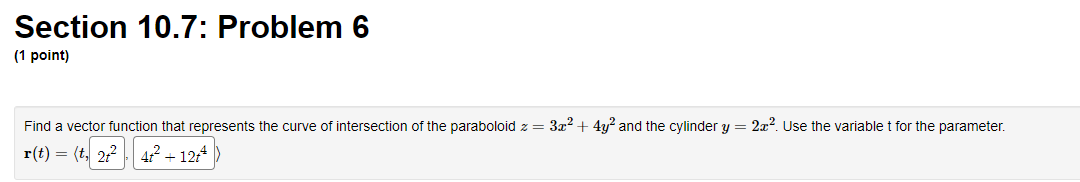
![(111(20t], 1/: + 3 (0ng s) \fSection 10.7: Problem 6 (1 point)](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667f8916b83be_198667f8916a328c.jpg)



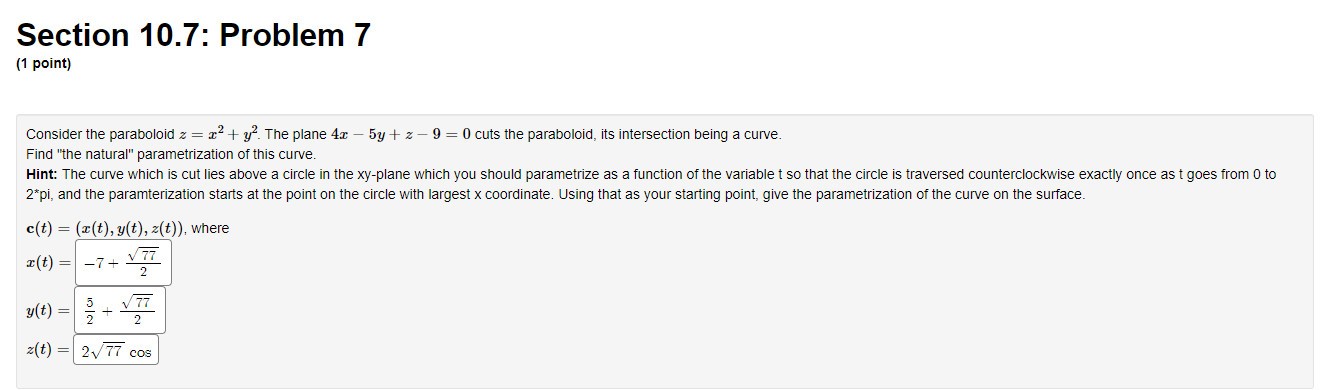
Section 10.7: Problem 1 [1 point} Find the domain of the 1vector functions, rm. listed below. You may use \"INF" for oo and use "IMF" for no as necessary, and use "U" for a union symbol if a union of intervals is needed. a} r(t) = (111(20t], 1/: + 3 (0ng s) \fSection 10.7: Problem 6 (1 point) Find a vector function that represents the curve of intersection of the paraboloid z = 3x + 4y and the cylinder y = 2x2. Use the variable t for the parameter. r(t) = (t, 2+2 At- + 12-Section 10.7: Problem 7 [1 point) Consider the paraboloid z = 22 + f. The plane 42 5y + z 9 = [I cuts the paraboloid, its intersecon being a curve. Find "the natural" parametrization of this curve. Hint: The curve which is cut lies above a circle in the xy-piane which you shouid parametrize as a function of the variable! so that the circle is traversed counterclockwise exactly once as 1 goes from 0 to 2*pi, and the paramterization starts at the point on the circle with largest in: coordinate Using that as your starting point, give the oaran'letrrzaon of the curve on the surface. c[t) : (:I:(t], y(t], z[t]], where Section 10.7: Problem 8 (1 point) Find the derivative of the vector function r(t) = In(12 -t?)i + v7+ ti - 8e "k 21 1 r'(t) = ( 12+2 V7+1 16e -2tSection 10.7: Problem 9 (1 point) For the given position vectors r(t) compute the unit tangent vector T(t) for the given value of t . A) Let r(t) = (cos 5t, sin 5t). Then T( )( V2 B) Let r(t) = (t2, +3 ) 9 Then T(3) = 2 85 85 C) Let r(t) = elite Stittk. -10 1 Then T(-2)= it it k . -20 + 162 16 + 1Section 10.8: Problem 3 (1 point) Consider the path r(t) = (8t, 4t , 41nt) defined for t > 0. Find the length of the curve between the points (8, 4, 0) and (40, 100, 4 1n(5)). 100 + 4 In(5)Section 10.8: Problem 4 (1 point) Consider the helix r(t) = (cos(6t), sin(6t), -4t). Compute, at t= #: A. The unit tangent vector T = 6 sin ( 6t) 6 cos( 6t) -4 B. The unit normal vector N = -6 cos( 6t) -6 sin (6t) 4 C. The unit binormal vector B = 7t sin - 14 cost 7tcos + 14 sin -8
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


