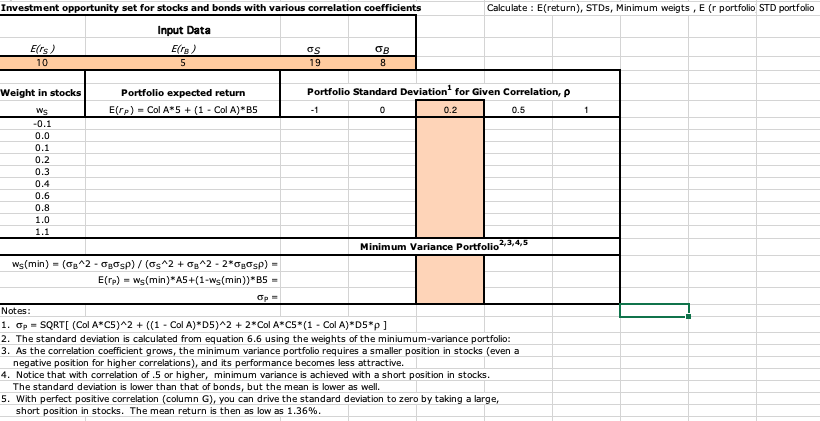
Calculate : E(return), STDs, Minimum weigts, E (r portfolio STD portfolio Investment opportunity set for stocks and bonds with various correlation coefficients Input Data Elts) Er) OS OB 10 5 19 8 Portfolio expected return E(TP) = Col A*5 + (1 - Col A)* B5 Portfolio Standard Deviation for Given Correlation, p 0 0.2 0.5 -1 1 Weight in stocks Ws -0.1 0.0 0.1 0.2 0.3 0.4 0.6 0.8 1.0 1.1 Minimum Variance Portfolio 2,3,4,5 ws(min) = (^2 - Ogosp)/(s^2 + 3^2 - 2*Ogosp) = E(TP) = ws(min)*A5+(1-ws(min))*B5 = Notes: 1. Op = SQRT (Col A*C5)^2 + ((1 - Col A)*D5)^2 + 2*Col A*C5*(1 - Col A)*D5*p] 2. The standard deviation is calculated from equation 6.6 using the weights of the miniumum-variance portfolio: 3. As the correlation coefficient grows, the minimum variance portfolio requires a smaller position in stocks (even a negative position for higher correlations), and its performance becomes less attractive. 4. Notice that with correlation of .5 or higher, minimum variance is achieved with a short position in stocks. The standard deviation is lower than that of bonds, but the mean is lower as well. 5. With perfect positive correlation (column G), you can drive the standard deviation to zero by taking a large, short position in stocks. The mean return is then as low as 1.36%