Calculate process mean (X-bar) and average range (R-bar).

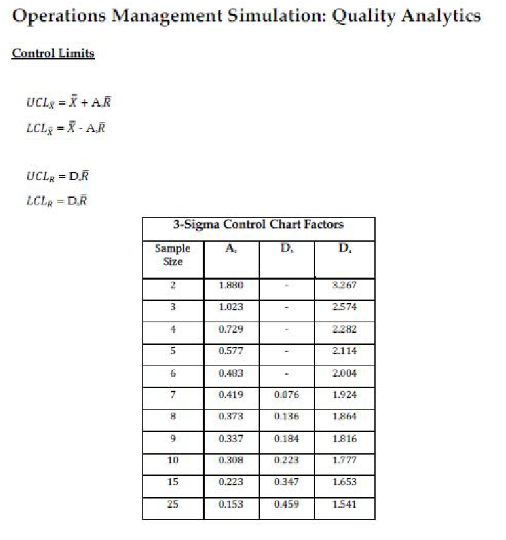
Find the LCL & UCL for an X-bar & R charts using the formulas in the Technology Primer (also available at the end of these instructions). Note that those formulas are not identical to the ones presented in the lecture and use shortcuts.

Shortcuts:

Data

X-BAR	R
29.17786824	9.846737279
29.41920731	7.326527512
26.22098903	5.215046078
31.03839537	12.98998725
31.18032898	5.610467967
30.14294911	12.6303436
29.73176862	9.211117517
29.78525681	7.220487228
31.5423799	11.44001586
29.29517815	9.302007383
30.66186928	9.232626559
31.25431636	8.484502318
31.78166657	8.401272151
29.45029354	3.58180589
26.69956619	10.19400761
29.77821565	6.622098194
28.45926431	7.915973057
28.90001457	12.28300571
28.68657517	7.569549402
29.37128721	6.853244314
29.70573775	6.219476693
30.64614946	11.96569981
29.84440924	4.698255732
28.32146463	7.958319562
30.6509834	8.341866803
27.47291893	5.462868937
28.59949126	7.702296312
27.94648943	3.379877443
30.12887304	5.842705467
28.20397336	8.737815376
30.57477517	7.939526439
30.72968499	5.334256249
29.66993886	4.895502668
30.78648695	6.733470967
29.94457654	7.310057675
30.83465746	4.817744952
32.5934681	8.312244228
29.4737988	6.922721662
31.70250892	6.651588067
30.35663744	8.074947054
31.26300923	10.33076303
29.89559144	7.407762757
31.04540068	13.07531516
29.29954717	9.377292266
29.6078817	8.554861982
30.80085648	9.835196489

What do the control limits tell us?

When a process is in-control, does it mean that it is producing an acceptable level of quality?

Operations Management Simulation: Quality Analytics Control Limits UCLX=X+ARLCLX=XA,R UCLR=DRLCLR=D,R "rocess Capability 1. Use visual inspection to determine whether the process mean is centered between the specification limits. 2. Calculate the process capability index. a. Use C^p if the process mean is centered between the specification limits. C^p=6aUSLLSL b. Use Cpk if the process mean is not centered between the specification limits. C^pk=min[3USL,3^USL] USL = Upper specifleation linlt LSL = Lower specifilcation llmit A^= Proceco mean, which 10 the centerline between the UCL and LCL. This can be caleulated by adding the UCL and LCL, then dividing by 2 = Process standard deviation, whech can be calculated from the control limito, as follows. Calculate the proceso standard error as the difference between elther of the control limils and the proceso mean, divided by 3 . Then, calculate the process standard deviation by multiplying the process otandard exror by n. 3. Higher values of C^p and C^pk indicate a more capable process. Experts recommend a process capability index of at least 1.33 for a two-sided specification. For a one-sided specification that consists of an upper linut only (for example, concentration) or a lower limit only (for example, for strength), the process is considered capable if the process capability index >1.25. Operations Management Simulation: Quality Analytics Control Limits UCLX=X+ARLCLX=XA,R UCLR=DRLCLR=D,R "rocess Capability 1. Use visual inspection to determine whether the process mean is centered between the specification limits. 2. Calculate the process capability index. a. Use C^p if the process mean is centered between the specification limits. C^p=6aUSLLSL b. Use Cpk if the process mean is not centered between the specification limits. C^pk=min[3USL,3^USL] USL = Upper specifleation linlt LSL = Lower specifilcation llmit A^= Proceco mean, which 10 the centerline between the UCL and LCL. This can be caleulated by adding the UCL and LCL, then dividing by 2 = Process standard deviation, whech can be calculated from the control limito, as follows. Calculate the proceso standard error as the difference between elther of the control limils and the proceso mean, divided by 3 . Then, calculate the process standard deviation by multiplying the process otandard exror by n. 3. Higher values of C^p and C^pk indicate a more capable process. Experts recommend a process capability index of at least 1.33 for a two-sided specification. For a one-sided specification that consists of an upper linut only (for example, concentration) or a lower limit only (for example, for strength), the process is considered capable if the process capability index >1.25