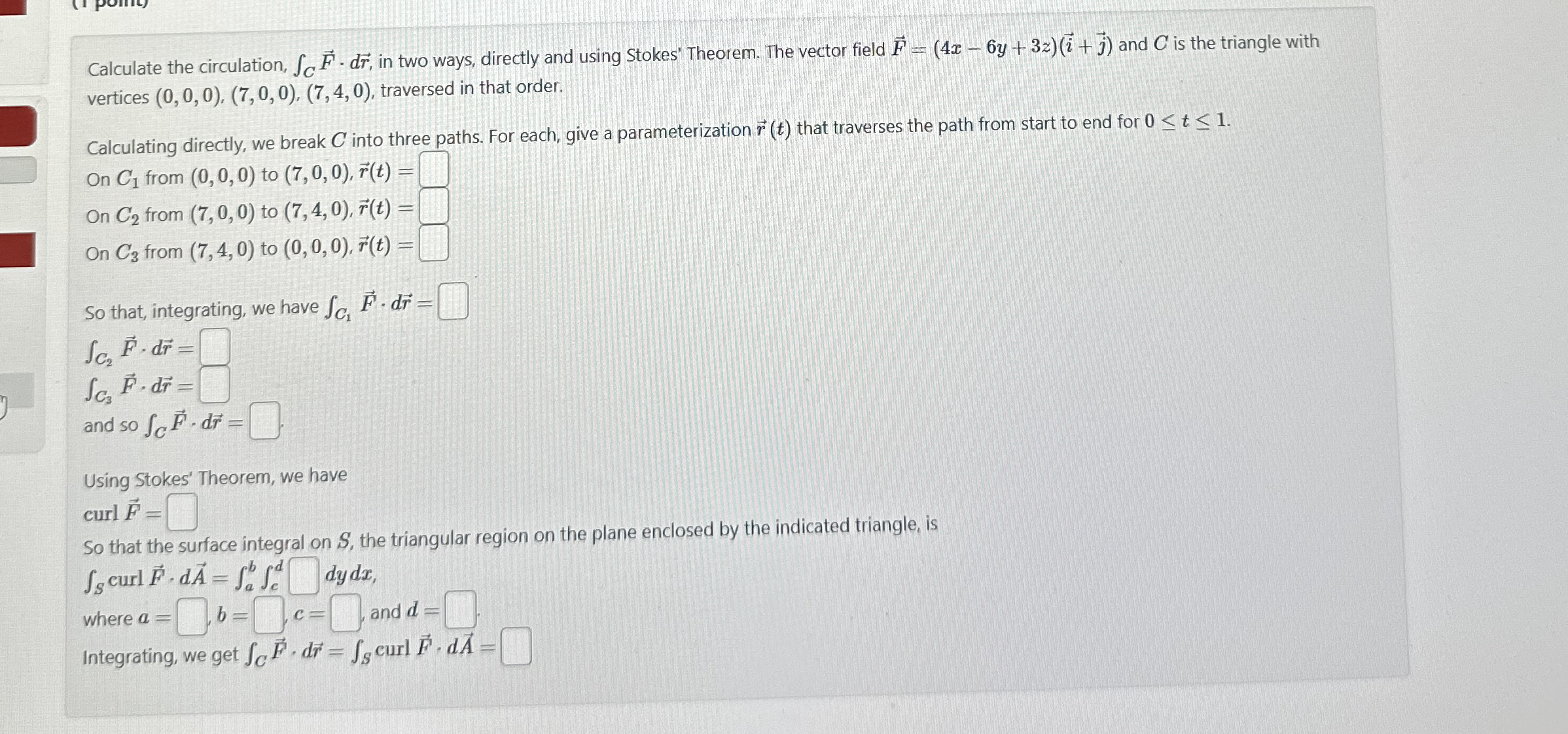
Calculate the circulation, ${\displaystyle \underset{C}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r),$ in two ways, directly and using Stokes' Theorem. The vector field vec$(F)=(4x-6y+3z)(vec(i)+$vec$(j))$ and $C$ is the triangle with vertices $(0,0,0),(7,0,0),(7,4,0),$ traversed in that order.

Calculating directly, we break $C$ into three paths. For each, give a parameterization vec$(r)(t)$ that traverses the path from start to end for $0t1.$

On $C_1$ from $(0,0,0)$ to $(7,0,0),$vec$(r)(t)=$

On $C_2$ from $(7,0,0)$ to $(7,4,0),$vec$(r)(t)=q,$

On $C_3$ from $(7,4,0)$ to $(0,0,0),$vec$(r)(t)=q,$

So that, integrating, we have ${\displaystyle \underset{C_1}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r)=$

${\displaystyle \underset{C_2}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r)=$

${\displaystyle \underset{C_3}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r)=$

and $so{\displaystyle \underset{C}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r)=$

$$

Using Stokes' Theorem, we have

curlvec$(F)=$

$$ So that the surface integral on $S,$ the triangular region on the plane enclosed by the indicated triangle, is

${\displaystyle \underset{S}{\overset{\phantom{}}{}}}$curlvec$(F)*dvec(A)={\displaystyle \underset{a}{\overset{b}{}}}{\displaystyle \underset{c}{\overset{d}{}}}dydx$

where $a=b=$ and $d=$

Integrating, we get ${\displaystyle \underset{C}{\overset{\phantom{}}{}}}$vec$(F)*dvec(r)={\displaystyle \underset{S}{\overset{\phantom{}}{}}}$curlvec$(F)*dvec(A)=$