Question: Calculate the following: (a) Compute the eigenvalues ( lambda_{1} ) and ( lambda_{2} ) of ( R ) and the corresponding eigenvectors ( gamma 1
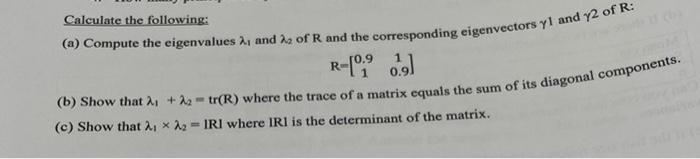
Calculate the following: (a) Compute the eigenvalues 1 and 2 of R and the corresponding eigenvectors 1 and 2 of R : R=[0.9110.9] (b) Show that 1+2=tr(R) where the trace of a matrix equals the sum of its diagonal components. (c) Show that 12=IRI where IRI is the determinant of the matrix
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


