Question: Calculus : 1-2 1. Find the derivative of the function f(x) = (x3 +x). 2. Find all critical numbers of the function f(x) = (2

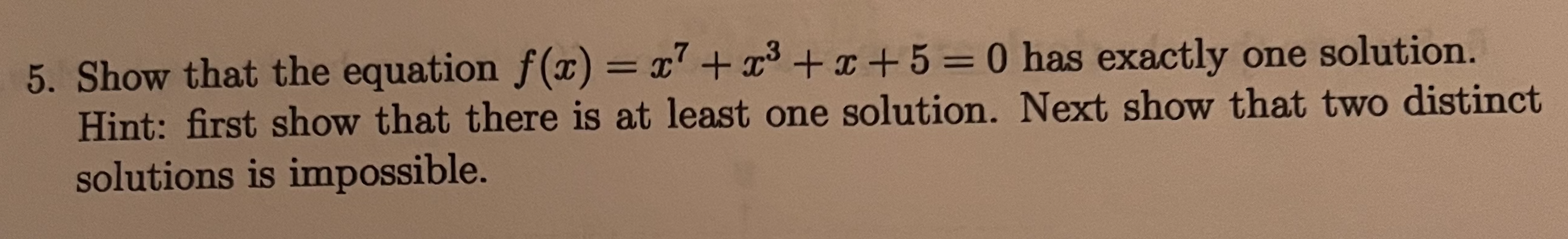


Calculus :
1-2

![impossible.7. [10 points] Suppose you are asked to design a rectangular box](https://s3.amazonaws.com/si.experts.images/answers/2024/06/66635920add35_912666359208d0c8.jpg)


1. Find the derivative of the function f(x) = (x3 +x). 2. Find all critical numbers of the function f(x) = (2 + 1)3(1 -I).5. Show that the equation f(x) = x7 +x3 +x +5 =0 has exactly one solution. Hint: first show that there is at least one solution. Next show that two distinct solutions is impossible.7. [10 points] Suppose you are asked to design a rectangular box of volume 1 m3 of minimal surface area if one side of the base is twice as long as the second side of the base. State the dimensions of the box of minimal surface area. Hint: draw a box with dimensions of the base x and 2x, and height y so that its volume V = 2x2y. Then compute the area of all sides (including top and bottom); add these and minimize this function.8. [20 points] Use calculus to graph the function f(I) = 1+12 1 _72. Indicate . I and y intercepts, . vertical and horizontal asymptotes (if any), . in/de-creasing; local/absolute max/min (if any). You must show work to justify your graph and conclusions. You can use decimal numbers to plot points (but mark them with exact values) y a . X Intercept = sqrt ( - 1) = i Y intercept = 1 b. vertical asymptotes = 1 and - 1 horizontal asymptotes = 0 C . none
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


