Calculus 2

Since chapter 8 is all about techniques of integration, I thought it would be fun to apply some of the basic techniques to deriving some common formulas for calculating the area of geometric shapes.In math, there is often more than one way to prove or determine something is true.I do not claim using calculus is the simplest way to derive (in other words, to determine) these formulas.But is certainly is a way.The idea is simple.Construct the definite integral needed to find the area of the geometric shape of your choosing.Then solve the integral to get the well-known formula for the area.I chose these because I thought the integral was very reasonable (except for circle, but we have a way to fix that).You can try to use the equation editor (x^2 in the menu) or use words like "the integral from 0 to 2 of (x^2+2)dx", for example.Then proceed to show the anti-derivative and evaluate at each of the limits to get the final formula.

Parallelogram:This diagram shows the parallelogram in a specific position to make the math easier.Notice the two linear functions have the same slope, but different y-intercepts, so they are parallel.The vertical lines x=0 and x=h are also parallel.Understand this will work for ANY parallelogram, just like the last one will work for any triangle.We use a slightly different approach here.I notice two functions and it appears the area of the parallelogram is between them.

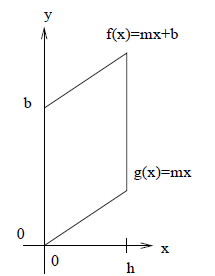
\f