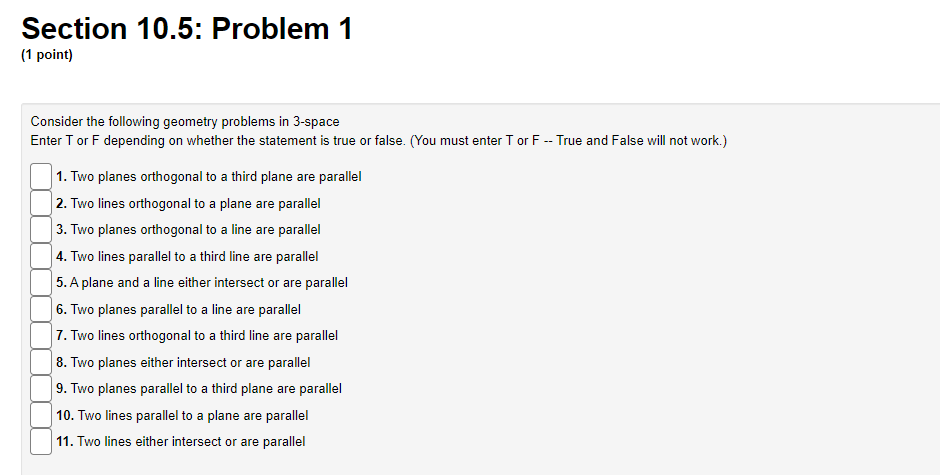
Question: Calculus 3 : Section 10.5: Problem 1 [1 point] Consider the following geometry problems in 3space Enter T or F depending on whether the statement
![Calculus 3 : Section 10.5: Problem 1 [1 point] Consider the](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d1285ed835_773667d1285d5dd3.jpg)





Calculus 3 :
![planes parallel to a third plane are parallel 1i]. Two lines parallel](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667d128958859_777667d128943286.jpg)






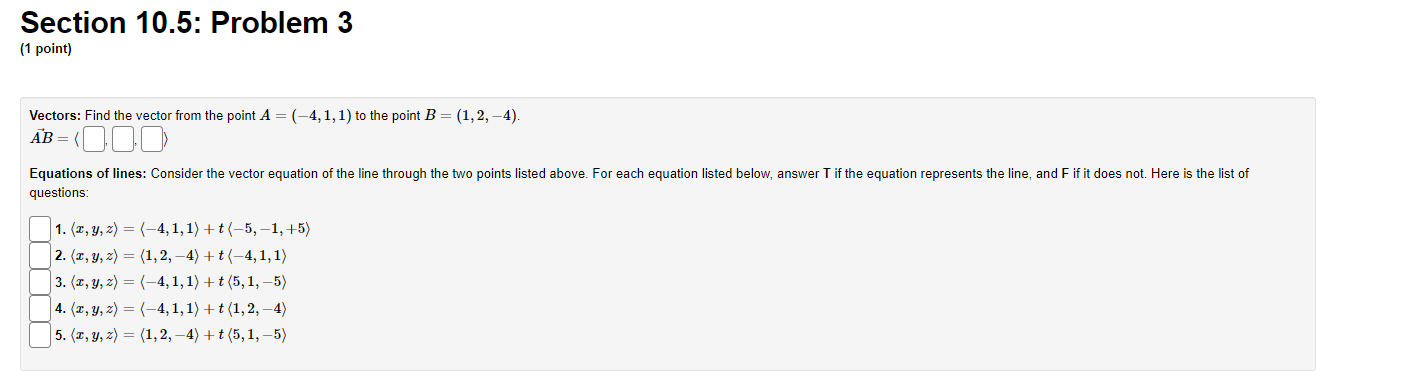
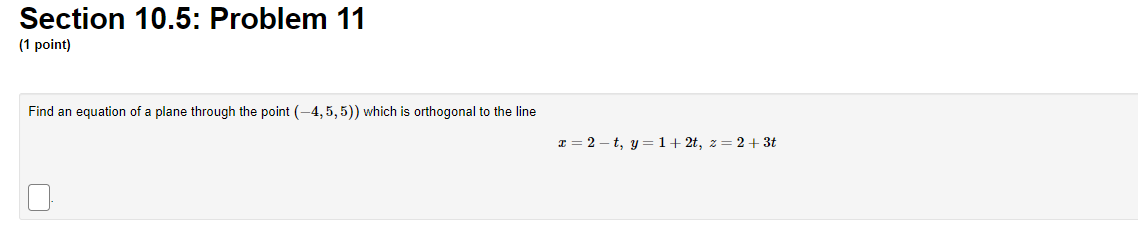
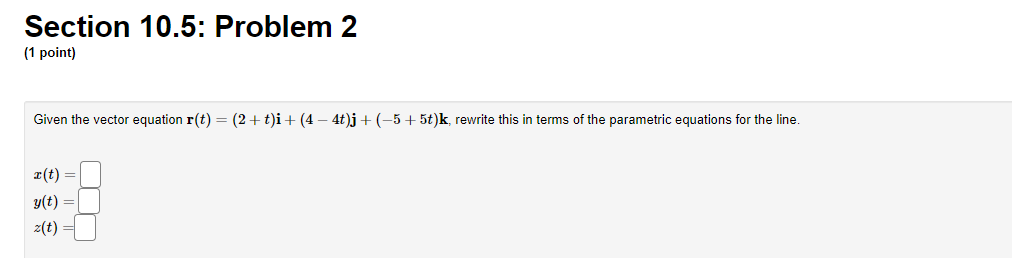
Section 10.5: Problem 1 [1 point] Consider the following geometry problems in 3space Enter T or F depending on whether the statement is true or false. [You must enter T or F -- True and False will not work.) 1. Two planes orlhogonal to a third plane are parallel 2. Two lines orthogonal to a plane are parallel 3. Two planes orlhogonal to a line are parallel 4. Two lines parallel to a third line are parallel 5. Aplane and a line either intersect or are parallel 6. Two planes parallel to a line are parallel T. Two lines orthogonal to a Third line are parallel 8. Two planes either intersect or are parallel 9. Two planes parallel to a third plane are parallel 1i]. Two lines parallel to a plane are parallel 11.Two lines either intersect or are parallel Section 10.5: Problem 3 (1 point) Vectors: Find the vector from the point A = (-4, 1, 1) to the point B = (1, 2, -4). AB =.DO Equations of lines: Consider the vector equation of the line through the two points listed above. For each equation listed below, answer T if the equation represents the line, and F if it does not. Here is the list of questions: 1. (I, y, z) = (-4, 1, 1) + t(-5, -1, +5) 2. (I, y, z) = (1,2, -4) + t (-4, 1, 1) 3. (x, y, z) = (-4, 1, 1) + t (5, 1, -5) 4. (1, y, z) = (-4, 1, 1) + t (1, 2, -4) 5. (1, y, z) = (1,2, -4) + t (5, 1, -5)Section 10.5: Problem 11 [1 point] Find an equation of a plane through the point [4,5, 5)) which is orthogonal to the line 2:2t, y=1+2t, z=2+3t C]. Section 10.5: Problem 2 [1 point] Given the vector equation 10$} 2 (2 + t)i + (4 4t)j + [5 + 5t)k, rewrite this in terms of the parametric equations for the line. 2U) = 9\") = z(t) Section 10.5: Problem 4 (1 point) Find the vector and parametric equations for the line through the point P = (1, -5, 3) and parallel to the vector (-1, -4, -1). Vector Form: r(t) = Parametric form (parameter t, and passing through P when t = 0): T = I(t) y = y(t) z = z(t)Section 10.5: Problem 5 (1 point) Consider the line which passes through the point P(-2, 5, 1), and which is parallel to the line : = 1 + 2t, y = 2 + 4t, z = 3 + 7t Find the point of intersection of this new line with each of the coordinate planes: cy-plane: ( cz-plane: yz-plane:Section 10.5: Problem 6 (1 point) Find the vector and parametric equations for the line through the point P(2, -4, 4) and orthogonal to the plane y - z + 32 = -2. Vector Form: r= Parametric form (parameter t, and passing through P when t = 0): I = :(t) y = y(t) z = z(t)Section 10.5: Problem 7 (1 point) Find the vector and parametric equations for the line through the point P(-4, -1, 5) and the point Q(0, -6, 4). Vector Form: r = (0.Q.5) + *( 0. Q. - 1) Parametric form (parameter t, and passing through P when t = 0): I = (t) y = y(t) 2 = 2(t)Section 10.5: Problem 8 (1 point) Find the vector equation for the line of intersection of the planes 5x + 5y - > = 2 and 5x + z = -3 r = , 0) + +(5, .>Section 10.5: Problem 9 (1 point) Consider the two lines L1:x= -2t, y = 1+2t, z = 3t and Lo : x=-5+1s, y = 4+1s, = =5+1s Find the point of intersection of the two lines. P =Section 10.5: Problem 10 (1 point) Determine whether the lines L1 : x = 23 + 6t, y = 5 +t, z=t and L2 : x = -9+7t y= -4+3t = =-11 + 4t intersect, are skew, or are parallel. If they intersect, determine the point of intersection; if not leave the remaining answer blanks empty. Do/are the lines: ? Point of inter
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


