Calculus

final result only is okay.

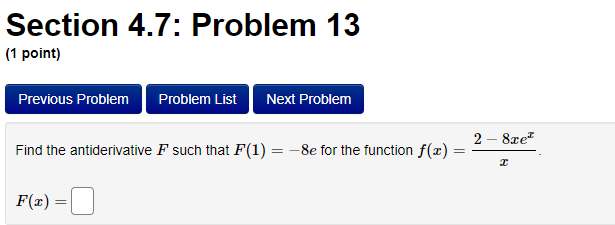
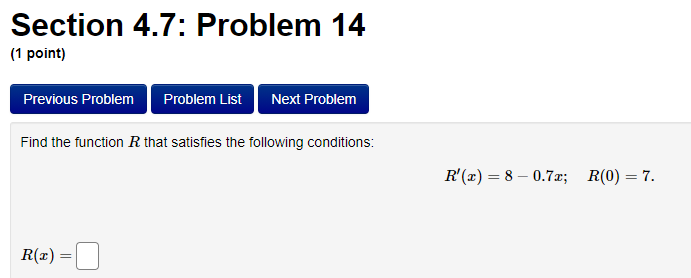
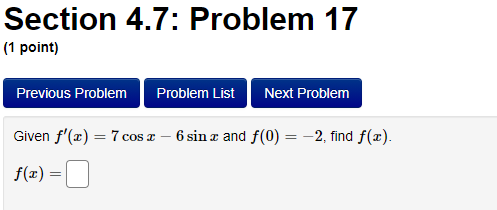
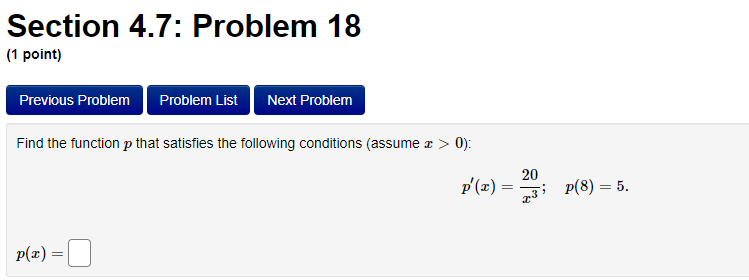
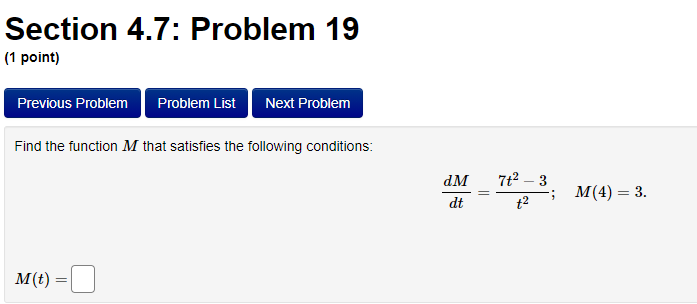
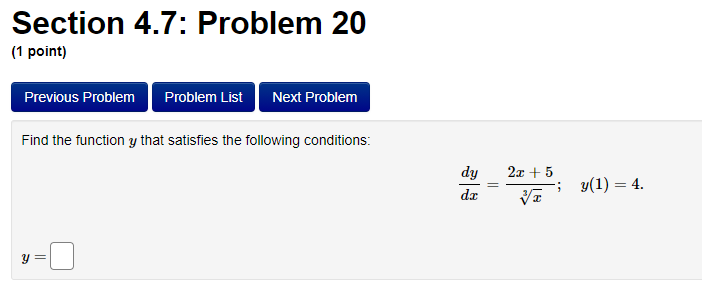
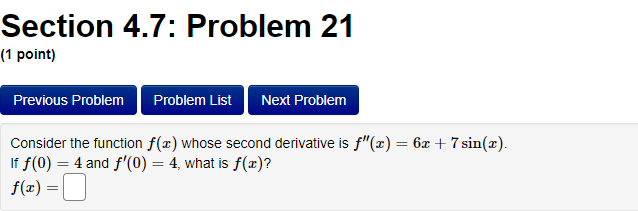
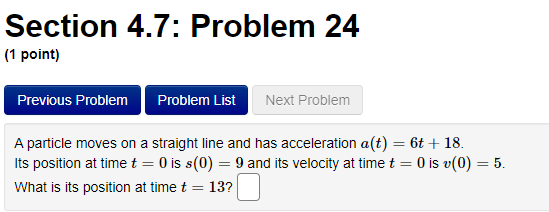
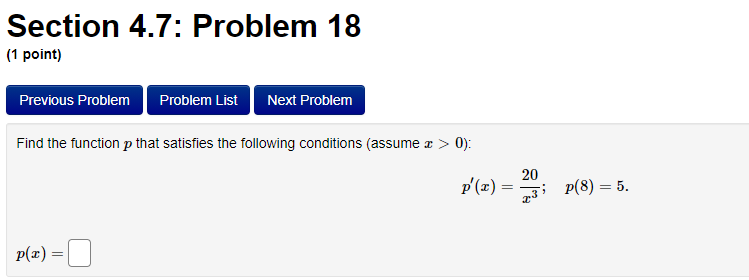
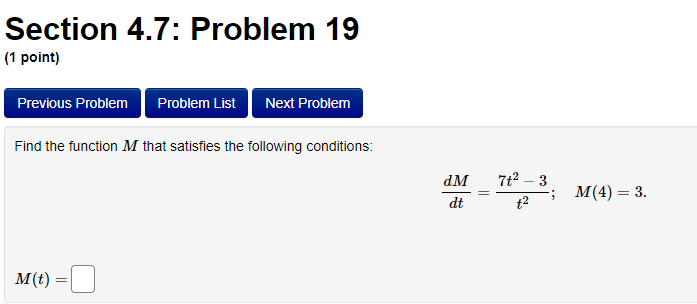
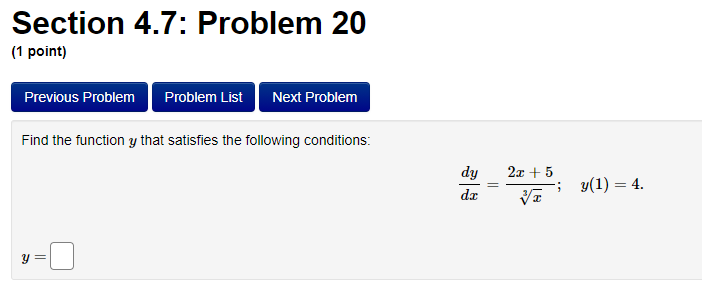
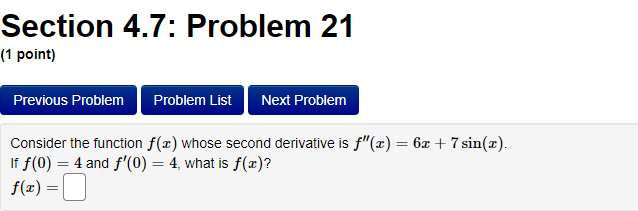
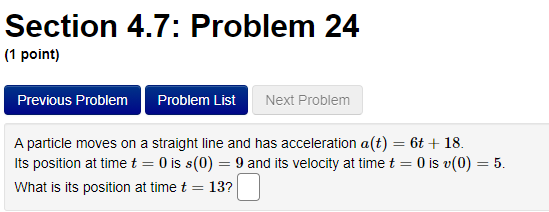
Section 4.7: Problem 13 (1 point) Previous Problem Problem List Next Problem 2- 8ret Find the antiderivative F such that F(1) = -8e for the function f(x ) = F(x) =Section 4.7: Problem 14 (1 point) Previous Problem Problem List Next Problem Find the function R that satisfies the following conditions: R'(x) = 8 - 0.7x; R(0) = 7. R(x) =Section 4.7: Problem 15 (1 point) Previous Problem Problem List Next Problem 5 7 Consider the function f(@ ) = 2 6:030. T Let F() be the antiderivative of f() with F(1) = 0. Then F(x) =Section 4.7: Problem 16 (1 point) Previous Problem Problem List Next Problem Consider the function f(t) = 7 sec (t) -6t Let F(t) be the antiderivative of f(t) with F(0) = 0. Then F(t) equalsSection 4.7: Problem 17 (1 point) Previous Problem Problem List Next Problem Given f'(x) = 7 cos x - 6 sin x and f(0) = -2, find f(x). f() =Section 4.7: Problem 18 (1 point) Previous Problem Problem List Next Problem Find the function p that satisfies the following conditions (assume > > 0): 20 P'(I) = 3; P(8) = 5. p(x) =Section 4.7: Problem 19 (1 point) Previous Problem Problem List Next Problem Find the function M that satisfies the following conditions: d.M 712 - 3 M(4) = 3. dt M(t) =Section 4.7: Problem 20 (1 point) Previous Problem Problem List Next Problem Find the function y that satisfies the following conditions: dy 2x + 5 -; y(1) = 4. 1/ =Section 4.7: Problem 21 (1 point) Previous Problem Problem List Next Problem Consider the function f(@) whose second derivative is f"(x) = 6x + 7 sin(x). If f(0) = 4 and f'(0) = 4, what is f(x)? f(x) =Section 4.7: Problem 22 (1 point) Previous Problem Problem List Next Problem If f" (x) = ez, f"(0) = 3 and f'(0) = 8, then f() = + C. Note that your answer should not contain a general constant.Section 4.7: Problem 23 (1 point) Previous Problem Problem List Next Problem Given that the graph of f() passes through the point (4, 6) and that the slope of its tangent line at (x, f(x)) is 3x + 3, what is f (4)?Section 4.7: Problem 24 (1 point) Previous Problem Problem List Next Problem A particle moves on a straight line and has acceleration a(t) = 6t + 18. Its position at time t = 0 is s(0) = 9 and its velocity at time t = 0 is v(0) = 5. What is its position at time t = 13